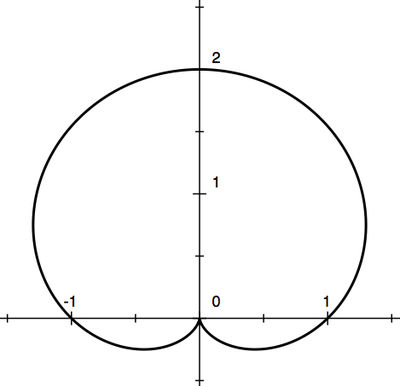
A curve is given in polar coordinates by

- a) Sketch the curve.
- b) Compute
 .
.
- c) Compute
 .
.
| Foundations:
|
How do you calculate  for a polar curve for a polar curve 
|
- Since
 we have we have
|

|
Solution:
(a)
(b)
| Step 1:
|
| First, recall we have
|

|
Since 
|

|
| Hence,
|

|
| Step 2:
|
Thus, we have

|
(c)
| Step 1:
|
We have 
|
So, first we need to find 
|
| We have
|

|
since  and and 
|
| Step 2:
|
Now, using the resulting formula for  we get we get
|

|
|
|
| Final Answer:
|
| (a) See Step 1 above for the graph.
|
(b) 
|
(c) 
|
Return to Sample Exam