007A Sample Midterm 2, Problem 4 Detailed Solution
Jump to navigation
Jump to search
Assume denotes the size of a population at time and that satisfies the equation:
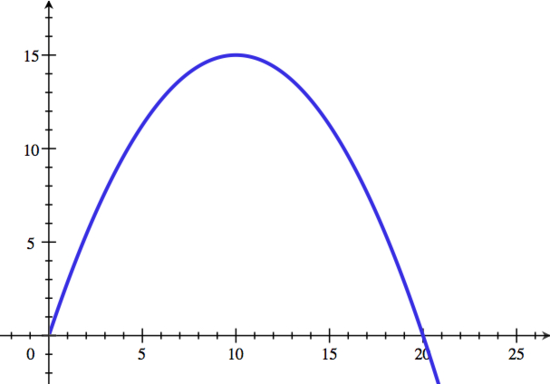
Let Graph as a function of and identify all equilibria. That is, all points where
| Background Information: |
|---|
| If then or |
Solution:
| Step 1: |
|---|
| First, we start by graphing |
| Step 2: |
|---|
| Now, we want to solve |
| Then, we have or |
| This means either or |
| Therefore, the equilibria occur at |
| and |
| Final Answer: |
|---|
| See Step 1 for graph |
| and |