004 Sample Final A, Problem 4
Jump to navigation
Jump to search
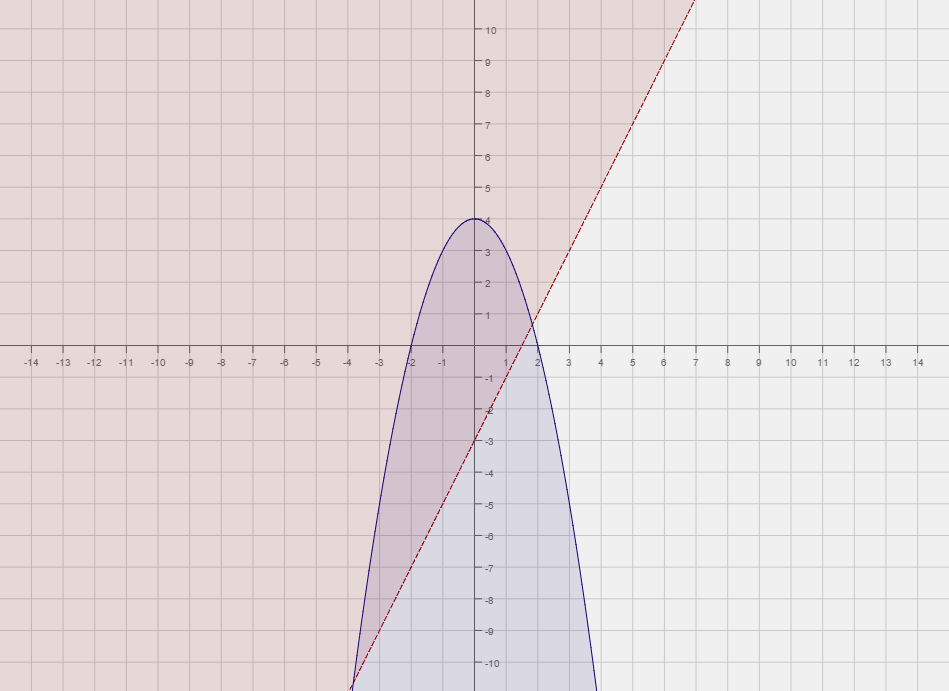
Graph the system of inequalities. Solution:
| Step 1: |
|---|
| First we replace the inequalities with equality. So , and . |
| Now we graph both functions. |
| Step 2: |
|---|
| Now that we have graphed both functions we need to know which region to shade with respect to each graph. |
| To do this we pick a point an equation and a point not on the graph of that equation. We then check if the |
| point satisfies the inequality or not. For both equations we will pick the origin. |
| Plugging in the origin we get, . Since the inequality is false, we shade the side of |
| that does not include the origin. We make the graph of dashed, since the inequality is strict. |
| Plugging in the origin we get . Since this inequality is true, we shade the side of that includes the origin. Here we make the graph of solid since the inequality sign is |
| Final Answer: |
|---|
| The final solution is the portion of the graph that below and above |
| The region we are referring to is shaded both blue and red. |
|








