004 Sample Final A, Problem 4

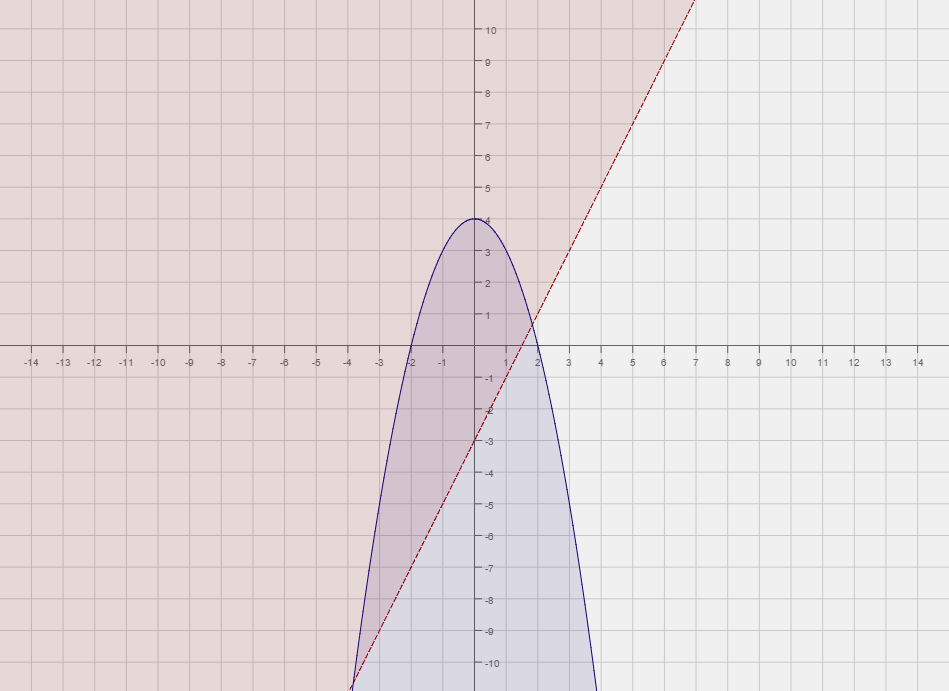
Graph the system of inequalities. $y>2x-3\qquad y\leq 4-x^{2}$ Solution:

ExpandStep 1:
First we replace the inequalities with equality. So $y=2x-3$, and $y=4-x^{2}$.
Now we graph both functions.

ExpandStep 2:
Now that we have graphed both functions we need to know which region to shade with respect to each graph.
To do this we pick a point an equation and a point not on the graph of that equation. We then check if the
point satisfies the inequality or not. For both equations we will pick the origin.
$y>2x-3:$ Plugging in the origin we get, $0>2(0)-3=-3$. Since the inequality is false, we shade the side of
$y=2x-3$ that does not include the origin. We make the graph of $y<\vert x\vert +1$ dashed, since the inequality is strict.
$y\leq 4-x^{2}:$ Plugging in the origin we get $0\leq 4-(0)^{2}=4$. Since this inequality is true, we shade the side of $y=4-x^{2}$ that includes the origin. Here we make the graph of $y=4-x^{2}$ solid since the inequality sign is $\leq$

ExpandFinal Answer:
The final solution is the portion of the graph that below $y=4-x^{2}$ and above $y=2x-3$
The region we are referring to is shaded both blue and red.

Return to Sample Exam