Prototype Calculus Question
Revision as of 17:52, 1 March 2015 by MathAdmin (talk | contribs) (Created page with "250px|right Find the volume of the solid obtained by rotating the area enclosed by <math> y=5-x </math> and <math style="vertical-align:-17%;"> y=25-x^2...")
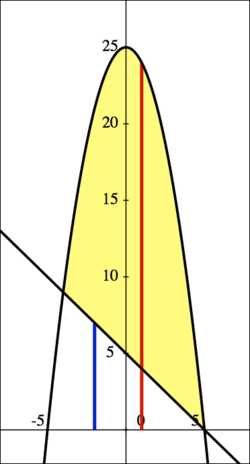
Find the volume of the solid obtained by rotating the area enclosed by and
around the x-axis.
| Foundations |
|---|
| Choose either shell or washer method. |
| Find the appropriate radii. |
| Determine the bounds of integration by finding when both functions have the same y value. |
| Solve the integral. |
Solution:
| Step 1: |
|---|
| Since we are rotating around the x-axis, the washer method would utilize tall rectangles with dx as their width. This seems like a reasonable choice, as these rectangles would be trapped between our two functions. |
| Step 2: |
|---|
| Since our rectangles will be trapped between the two functions, and will be rotated around the x-axis (where ,) we find |
| the inner radius is , represented by the blue line, while |
| the outer radius is , represented by the red line. |
| Step 3: |
|---|
| We must set the two functions equal, and solve. More to follow... |