Prototype Calculus Question

Find the volume of the solid obtained by rotating the area enclosed by $y=5-x$ and $y=25-x^{2}$
around the x-axis.

Foundations
• Choose either shell or washer method.
• Find the appropriate radii.
• Determine the bounds of integration by finding when both functions have the same y value.
• Using the determined values, set up and solve the integral.

Solution:

Step 1:
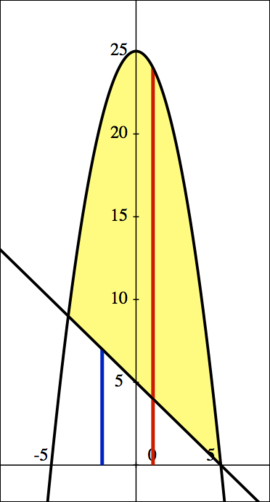
Choosing the Approach:   Since we are rotating around the x-axis, the washer method would utilize tall rectangles with dx as their width. This seems like a reasonable choice, as these rectangles would be trapped between our two functions as x varies over the enclosed region, allowing us to solve a single integral. Note that the washer method will require an inner and outer radius, as well as bounds of integration, in order to evaluate the integral
$V=\pi \int _{x_{1}}^{\,x_{2}}R^{2}-r^{2}\,dx$

Step 2:
Finding the Radii:  Since our rectangles will be trapped between the two functions, and will be rotated around the x-axis (where y = 0), we find
the inner radius is $r=5-x$, represented by the blue line, while
the outer radius is $R=25-x^{2}$, represented by the red line.

Step 3:
Finding the Bounds of Integration:   We must set the two functions equal, and solve. If
$5-x=25-x^{2},$
then by moving all terms to the left hand side and factoring,
$x^{2}-x-20=(x+4)(x-5)=0,$
so we have -4 and 5 as solutions. These are our bounds of integration.

Step 4:
Evaluating the Integral:   Using the earlier steps, we have
$V=\pi \int _{x_{1}}^{\,x_{2}}R^{2}-r^{2}\,dx$
$=\pi \int _{-4}^{\,5}(25-x^{2})^{2}-(5-x)^{2}\,dx$
$=\pi \int _{-4}^{\,5}625-50x^{2}+x^{4}-(25-10x+x^{2})\,dx$
$=\pi \int _{-4}^{\,5}600-51x^{2}+x^{4}+10x\,dx$
$=\pi \int _{-4}^{\,5}600-51x^{2}+x^{4}+10x\,dx$
$=\pi {\biggr (}600x-51\cdot {\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+10\cdot {\frac {x^{2}}{2}}{\biggr )}{\biggr |}_{x=-4}^{5}$
$={\frac {15,309}{5}}\,\pi .$