Math 22 Graph of Equation

The Graph of an Equation

The graph of an equation is the set of all points that are solutions of the equation.

In this section, we use point-plotting method. With this method, you construct a table of values that consists of several solution points of the equation

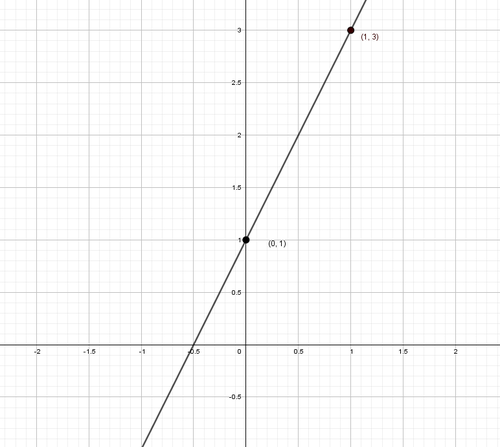
For example, sketch the graph of $y=2x+1$. We can construct the table below by plugging points for $x$.

x	0	1	2	3
y=2x+1	1	3	5	7

So, we can sketch the graph from those order pairs.

Intercepts of a Graph

Some solution points have zero as either the $x$-coordinate or the $y$-coordinate. These points are called intercepts because they are the points at which the graph intersects the $x$- or $y$-axis.

 To find $x$-intercepts, let $y$ be zero and solve the equation for $x$.
 
 To find $y$-intercepts, let $x$ be zero and solve the equation for $y$.

Example Find the x-intercepts and y-intercepts of the graph $y=x^{2}-2x$

Solution:
x-intercept: Let $y=0$, so $x^{2}-2x=0$, hence $x(x-2)=0$, therefore, $x=0$ or $x=2$
y-intercept: Let $x=0$, so $y=(0)^{2}-2(0)=0$
Answer: $(0,0)$ and $(2,0)$ are x-intercepts
$(0,0)$ is y-intercept

Circles

 The standard form of the equation of a circle is
 
 $(x-h)^{2}+(y-k)^{2}=r^{2}$
 
 The point $(h,k)$ is the center of the circle, and the positive number $r$ is the radius of the circle

In general, to write an equation of a circle, we need to know radius $r$ and the center $(h,k)$.

Example Given that the point $(2,1)$ is on the circle centered at (3,4). Find the equation of a circle.

Solution:
We need to know the radius and the center in order to write the equation. The center is given at $(3,4)$. It is left to find the radius.
Radius is the distance between the center and a point on the circle. So, radius $r$ is the distance between $(2,1)$ and $(3,4)$.
So, $r={\sqrt {(2-3)^{2}+(1-4)^{2}}}={\sqrt {1+9}}={\sqrt {10}}$
Now, write the equation of the circle with radius $r={\sqrt {10}}$ and center $(3,4)$ to get:
$(x-3)^{2}+(y-4)^{2}=10$

Notes

Distance $D$ between $(x_{1},y_{1})$ and $(x_{2},y_{2})$ can be calculated by using $D={\sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}}$

This page were made by Tri Phan