Difference between revisions of "004 Sample Final A, Problem 4"
Jump to navigation
Jump to search
(Created page with "<span class="exam"> Graph the system of inequalities. <math>y > 2x - 3 \qquad y \le 4-x^2</math> {| class="mw-collapsible mw-collapsed" style = "text-align:left;" ! Foundation...") |
|||
| Line 1: | Line 1: | ||
<span class="exam"> Graph the system of inequalities. <math>y > 2x - 3 \qquad y \le 4-x^2</math> | <span class="exam"> Graph the system of inequalities. <math>y > 2x - 3 \qquad y \le 4-x^2</math> | ||
| + | Solution: | ||
| + | |||
{| class="mw-collapsible mw-collapsed" style = "text-align:left;" | {| class="mw-collapsible mw-collapsed" style = "text-align:left;" | ||
| − | ! | + | ! Step 1: |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | | | + | |First we replace the inequalities with equality. So <math>y = \vert x\vert + 1</math>, and <math>x^2 + y^2 = 9</math>. |
|- | |- | ||
| − | |we | + | |Now we graph both functions. |
|} | |} | ||
| − | + | {| class="mw-collapsible mw-collapsed" style = "text-align:left;" | |
| − | + | ! Step 2: | |
| − | |||
| − | {| class = "mw-collapsible mw-collapsed" style = "text-align:left;" | ||
| − | ! Step | ||
|- | |- | ||
| − | | | + | |Now that we have graphed both functions we need to know which region to shade with respect to each graph. |
|- | |- | ||
| − | | | + | |To do this we pick a point an equation and a point not on the graph of that equation. We then check if the |
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | | | + | |point satisfies the inequality or not. For both equations we will pick the origin. |
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | | | + | |<math>y < \vert x\vert + 1:</math> Plugging in the origin we get, <math>0 < \vert 0\vert + 1 = 1</math>. Since the inequality is satisfied shade the side of |
|- | |- | ||
| − | | | + | |<math>y < \vert x\vert + 1</math> that includes the origin. We make the graph of <math>y < \vert x\vert + 1</math>, since the inequality is strict. |
|- | |- | ||
| − | | | + | |<math>x^2 + y^2 \le 9:</math> <math>(0)^2 +(0)^2 = 0 \le 9</math>. Once again the inequality is satisfied. So we shade the inside of the circle. |
|- | |- | ||
| − | | | + | |We also shade the boundary of the circle since the inequality is <math>\le</math> |
|} | |} | ||
| − | {|class = "mw-collapsible mw-collapsed" style = "text-align:left;" | + | {| class="mw-collapsible mw-collapsed" style = "text-align:left;" |
| − | ! | + | ! Final Answer: |
|- | |- | ||
| − | | | + | |The final solution is the portion of the graph that below <math>y = \vert x\vert + 1</math> and inside <math> x^2 + y^2 = 9</math> |
|- | |- | ||
| − | | | + | |The region we are referring to is shaded both blue and red. |
|- | |- | ||
| − | | | + | |[[File:8A_Final_5.png]] |
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[004 Sample Final A|<u>'''Return to Sample Exam</u>''']] | [[004 Sample Final A|<u>'''Return to Sample Exam</u>''']] | ||
Revision as of 09:01, 2 June 2015
Graph the system of inequalities. Solution:
| Step 1: |
|---|
| First we replace the inequalities with equality. So , and . |
| Now we graph both functions. |
| Step 2: |
|---|
| Now that we have graphed both functions we need to know which region to shade with respect to each graph. |
| To do this we pick a point an equation and a point not on the graph of that equation. We then check if the |
| point satisfies the inequality or not. For both equations we will pick the origin. |
| Plugging in the origin we get, . Since the inequality is satisfied shade the side of |
| that includes the origin. We make the graph of , since the inequality is strict. |
| . Once again the inequality is satisfied. So we shade the inside of the circle. |
| We also shade the boundary of the circle since the inequality is |
| Final Answer: |
|---|
| The final solution is the portion of the graph that below and inside |
| The region we are referring to is shaded both blue and red. |
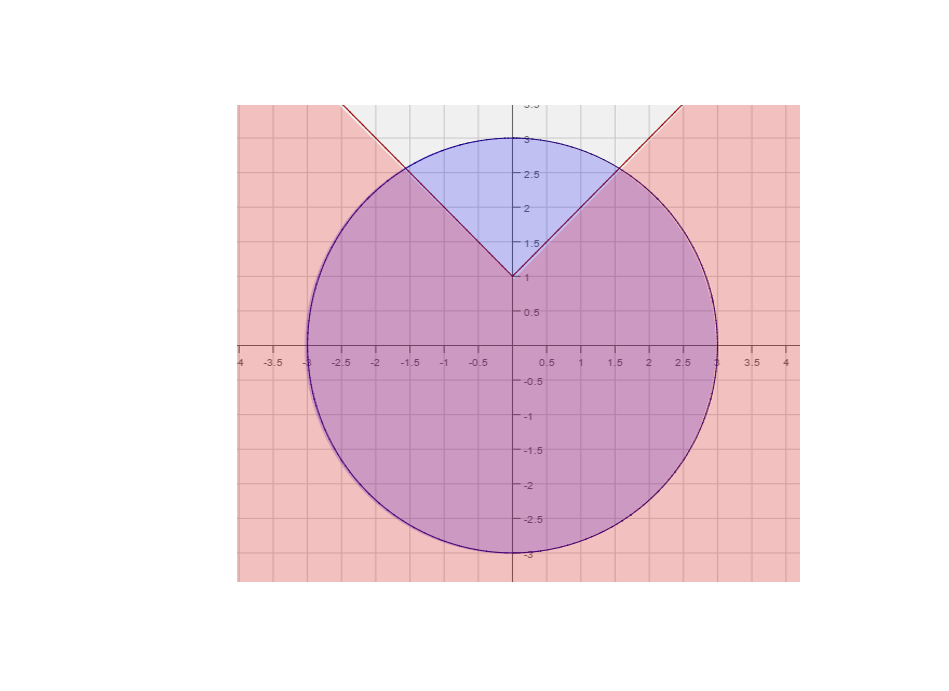
|








