Difference between revisions of "022 Exam 2 Sample B, Problem 10"
Jump to navigation
Jump to search
(Created page with "right|550px <span class="exam">'''Use calculus to set up and solve the word problem:''' A fence is to be built to enclose a rectangular region of 48...") |
|||
| Line 1: | Line 1: | ||
| − | [[File:022_2_B_10GP.png|right| | + | [[File:022_2_B_10GP.png|right|370px]] |
<span class="exam">'''Use calculus to set up and solve the word problem:''' | <span class="exam">'''Use calculus to set up and solve the word problem:''' | ||
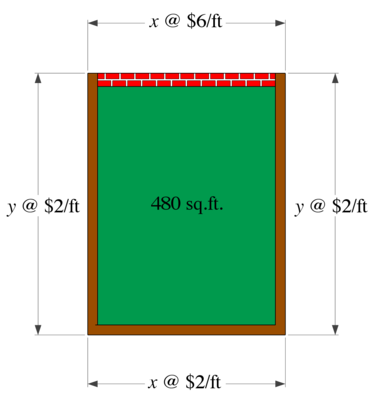
A fence is to be built to enclose a rectangular region of 480 square feet. The fencing material along three sides cost $2 per foot. The fencing material along the 4<sup>th</sup> side costs $6 per foot. Find the most economical dimensions of the region (that is, minimize the cost). | A fence is to be built to enclose a rectangular region of 480 square feet. The fencing material along three sides cost $2 per foot. The fencing material along the 4<sup>th</sup> side costs $6 per foot. Find the most economical dimensions of the region (that is, minimize the cost). | ||
| + | |||
| + | {| class="mw-collapsible mw-collapsed" style = "text-align:left;" | ||
| + | !Foundations: | ||
| + | |- | ||
| + | |As with all geometric word problems, it helps to start with a picture. Using the variables <math style="vertical-align: 0%">x</math> and <math style="vertical-align: -20%">y</math> as shown in the image, we need to remember the equations of a rectangle for area: | ||
| + | |- | ||
| + | | | ||
| + | ::<math>A\,=\,xy.</math> | ||
| + | |- | ||
| + | |However, we need to construct a new function to describe cost: | ||
| + | |- | ||
| + | | | ||
| + | ::<math>C\,=\,(2+6)x+(2+2)y\,=\,8x+4y.</math> | ||
| + | |- | ||
| + | |Since we want to minimize cost, we will have to rewrite it as a function of a single variable, and then find when the first derivative is zero. From this, we will find the dimensions which provide the minimum cost. | ||
| + | |} | ||
| + | |||
| + | '''Solution:''' | ||
| + | |||
| + | {| class="mw-collapsible mw-collapsed" style = "text-align:left;" | ||
| + | !Step 1: | ||
| + | |- | ||
| + | |'''Express one variable in terms of the other:''' Since we know that the area is 480 square feet and <math style="vertical-align: -20%">A\,=\,xy</math>, we can solve for <math style="vertical-align: -15%">y</math> in terms of <math style="vertical-align: 0%">x</math>. Since <math style="vertical-align: -20%">480\,=\,xy</math>, we find that <math style="vertical-align: -20%">y=480/x</math>. | ||
| + | |} | ||
| + | |||
| + | {| class="mw-collapsible mw-collapsed" style = "text-align:left;" | ||
| + | !Step 2: | ||
| + | |- | ||
| + | |'''Find an expression for cost in terms of one variable:''' Now, we can use the substitution from part 1 to find | ||
| + | |- | ||
| + | | | ||
| + | ::<math>C(x)\,=\,8x+4y\,=\,8x+4\cdot \frac{480}{x}\,=\,8x+\frac{1920}{x}.</math> | ||
| + | |} | ||
| + | |||
| + | {| class="mw-collapsible mw-collapsed" style = "text-align:left;" | ||
| + | !Step 3: | ||
| + | |- | ||
| + | |'''Find the derivative and its roots:''' We can apply the power rule term-by-term to find | ||
| + | |- | ||
| + | | | ||
| + | ::<math>C'(x)\,=\,8-\frac{1920}{x^2}\,=\,8\left(1-\frac{240}{x^2}\right).</math> | ||
| + | |- | ||
| + | |This derivative is zero precisely when <math style="vertical-align: -10%">x=4\sqrt{15}</math>, which occurs when <math style="vertical-align: -20%">y=8\sqrt{15}</math>, and these are the values that will minimize cost. Also, don't forget the units - feet! | ||
| + | |} | ||
| + | |||
| + | {| class="mw-collapsible mw-collapsed" style = "text-align:left;" | ||
| + | !Final Answer: | ||
| + | |- | ||
| + | |The cost is minimized when the dimensions are <math style="vertical-align: -5%">8\sqrt{15}</math> feet by <math style="vertical-align: -5%">4\sqrt{15}</math> feet. Note that the side with the most expensive fencing is the shorter one. | ||
| + | |} | ||
| + | |||
| + | [[022_Exam_2_Sample_B|'''<u>Return to Sample Exam</u>''']] | ||
Revision as of 11:23, 17 May 2015
Use calculus to set up and solve the word problem: A fence is to be built to enclose a rectangular region of 480 square feet. The fencing material along three sides cost $2 per foot. The fencing material along the 4th side costs $6 per foot. Find the most economical dimensions of the region (that is, minimize the cost).
| Foundations: |
|---|
| As with all geometric word problems, it helps to start with a picture. Using the variables and as shown in the image, we need to remember the equations of a rectangle for area: |
|
|
| However, we need to construct a new function to describe cost: |
|
|
| Since we want to minimize cost, we will have to rewrite it as a function of a single variable, and then find when the first derivative is zero. From this, we will find the dimensions which provide the minimum cost. |
Solution:
| Step 1: |
|---|
| Express one variable in terms of the other: Since we know that the area is 480 square feet and , we can solve for in terms of . Since , we find that . |
| Step 2: |
|---|
| Find an expression for cost in terms of one variable: Now, we can use the substitution from part 1 to find |
|
|
| Step 3: |
|---|
| Find the derivative and its roots: We can apply the power rule term-by-term to find |
|
|
| This derivative is zero precisely when , which occurs when , and these are the values that will minimize cost. Also, don't forget the units - feet! |
| Final Answer: |
|---|
| The cost is minimized when the dimensions are feet by feet. Note that the side with the most expensive fencing is the shorter one. |