022 Exam 2 Sample B, Problem 10

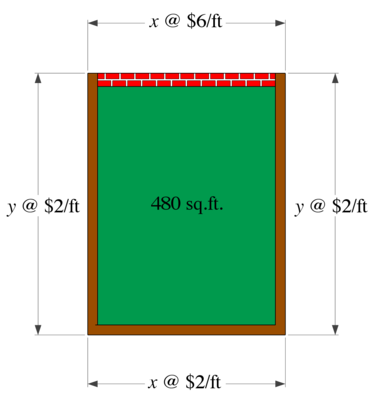
Use calculus to set up and solve the word problem: A fence is to be built to enclose a rectangular region of 480 square feet. The fencing material along three sides cost $2 per foot. The fencing material along the 4^th side costs $6 per foot. Find the most economical dimensions of the region (that is, minimize the cost).

Foundations:
As with all geometric word problems, it helps to start with a picture. Using the variables $x$ and $y$ as shown in the image, we need to remember the equation for the area of a rectangle:
$A\,=\,xy.$
However, we need to construct a new function to describe cost:
$C\,=\,(2+6)x+(2+2)y\,=\,8x+4y.$
Since we want to minimize cost, we will have to rewrite it as a function of a single variable, and then find when the first derivative is zero. From this, we will find the dimensions which provide the minimum cost.

 Solution:

Step 1:
Express one variable in terms of the other: Since we know that the area is 480 square feet and $A\,=\,xy$, we can solve for $y$ in terms of $x$. Since $480\,=\,xy$, we find that $y=480/x$.

Step 2:
Find an expression for cost in terms of one variable: Now, we can use the substitution from step 1 to find
$C(x)\,=\,8x+4y\,=\,8x+4\cdot {\frac {480}{x}}\,=\,8x+{\frac {1920}{x}}.$

Step 3:
Find the derivative and its roots: We can apply the power rule term-by-term to find
$C'(x)\,=\,8-{\frac {1920}{x^{2}}}\,=\,8\left(1-{\frac {240}{x^{2}}}\right).$
This derivative is zero precisely when $x=4{\sqrt {15}}$, which occurs when $y=8{\sqrt {15}}$, and these are the values that will minimize cost. Also, don't forget the units - feet!

Final Answer:
The cost is minimized when the dimensions are $8{\sqrt {15}}$ feet by $4{\sqrt {15}}$ feet. Note that the side with the most expensive fencing is the shorter one.

Return to Sample Exam