Difference between revisions of "009C Sample Final 3, Problem 9"
(Created page with "right|350px <span class="exam">A wheel of radius 1 rolls along a straight line, say the <math>x</math>-axis. A point <math style="vertica...") |
|||
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | [[File:9CSF3_9a_GP.png|right| | + | [[File:9CSF3_9a_GP.png|right|400px]] |
<span class="exam">A wheel of radius 1 rolls along a straight line, say the <math>x</math>-axis. A point <math style="vertical-align: 0px">P</math> is located halfway between the center of the wheel and the rim. As the wheel rolls, <math style="vertical-align: 0px">P</math> traces a curve. Find parametric equations for the curve. | <span class="exam">A wheel of radius 1 rolls along a straight line, say the <math>x</math>-axis. A point <math style="vertical-align: 0px">P</math> is located halfway between the center of the wheel and the rim. As the wheel rolls, <math style="vertical-align: 0px">P</math> traces a curve. Find parametric equations for the curve. | ||
| Line 12: | Line 12: | ||
Essentially, equations of motion can often be broken into parts, and | Essentially, equations of motion can often be broken into parts, and | ||
then added up. | then added up. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| Line 28: | Line 20: | ||
!Step 1: | !Step 1: | ||
|- | |- | ||
| − | |If a wheel of radius one is resting at the origin, its axis will be at the point <math style="vertical-align: -5px">(1,0). </math> For this solution, we will assume the point <math style="vertical-align: 0px">P </math> is below the axle, although the problem does not state the position of <math style="vertical-align: 0px">P </math>. When the wheel rotates clockwise, it will move to the right. Since the length of the arc defined by an angle <math style="vertical-align: 0px">\theta </math> on a circle of radius <math style="vertical-align: 0px">R </math> is <math style="vertical-align: -4px">L=R\cdot\theta=1\cdot\theta=\theta, </math> & | + | |If a wheel of radius one is resting at the origin, its axis will be at the point <math style="vertical-align: -5px">(1,0). </math> For this solution, we will assume the point <math style="vertical-align: 0px">P </math> is below the axle, although the problem does not state the position of <math style="vertical-align: 0px">P </math>. When the wheel rotates clockwise, it will move to the right. Since the length of the arc defined by an angle <math style="vertical-align: 0px">\theta </math> on a circle of radius <math style="vertical-align: 0px">R </math> is <math style="vertical-align: -4px">L=R\cdot\theta=1\cdot\theta=\theta, </math> the wheel will roll forward the length of the arc, which is just <math style="vertical-align: 0px">\theta. </math> |
| − | Moreover, the axle's <math style="vertical-align: 0px">x </math> position will change in the same manner, | + | Moreover, the axle's <math style="vertical-align: 0px">x </math> position will change in the same manner, while the height of the axle will always be fixed at <math style="vertical-align: -4px">y=1 </math>. This means we can describe the position of the axle as a function of <math style="vertical-align: -4px">\theta, </math> or |
| − | while the height of the axle will always be fixed at <math style="vertical-align: -4px">y=1 </math>. This | ||
| − | means we can describe the position of the axle as a function of <math style="vertical-align: -4px">\theta, </math> | ||
| − | or | ||
:: <math>a(\theta)\,=\,(\theta,1). </math> | :: <math>a(\theta)\,=\,(\theta,1). </math> | ||
| Line 42: | Line 31: | ||
!Step 2: | !Step 2: | ||
|- | |- | ||
| − | |Since the wheel is rotating, we also know that our point <math style="vertical-align: 0px">P </math> will rotate around the axle. As described in the problem, it is halfway | + | |Since the wheel is rotating, we also know that our point <math style="vertical-align: 0px">P </math> will rotate around the axle. As described in the problem, it is halfway between the rim and the center/axle, so it is <math style="vertical-align: -5px">1/2 </math> unit away from the axle, and will rotate clockwise. Using our trig relations (while looking at the image), we find that the position of <math style="vertical-align: 0px">P </math> relative to the axle can be described as |
| − | between the rim and the center/axle, so it is <math style="vertical-align: - | ||
:: <math>p(\theta)\,=\,\left(-\frac{1}{2}\sin\theta,-\frac{1}{2}\cos\theta\right). </math> | :: <math>p(\theta)\,=\,\left(-\frac{1}{2}\sin\theta,-\frac{1}{2}\cos\theta\right). </math> | ||
| − | Notice that when <math style="vertical-align: -4px">\theta=0, </math> the point would be at the position | + | Notice that when <math style="vertical-align: -4px">\theta=0, </math> the point would be at the position |
:: <math>p(0)\,=\,\left(-\frac{1}{2}\sin0,-\frac{1}{2}\cos0\right)\,=\,\left(0,-\frac{1}{2}\right), </math> | :: <math>p(0)\,=\,\left(-\frac{1}{2}\sin0,-\frac{1}{2}\cos0\right)\,=\,\left(0,-\frac{1}{2}\right), </math> | ||
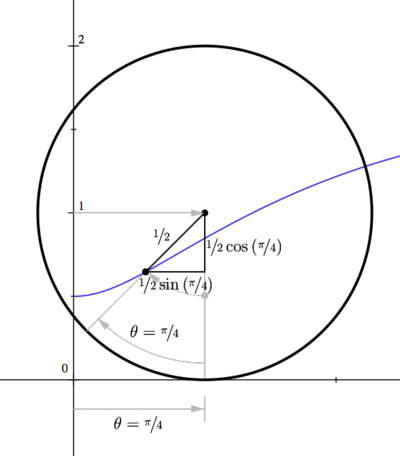
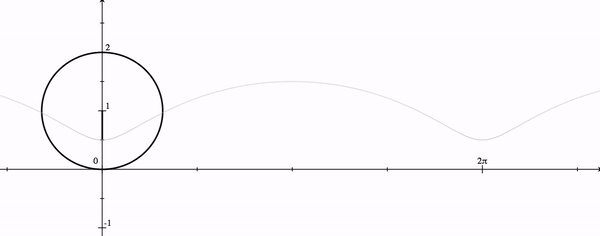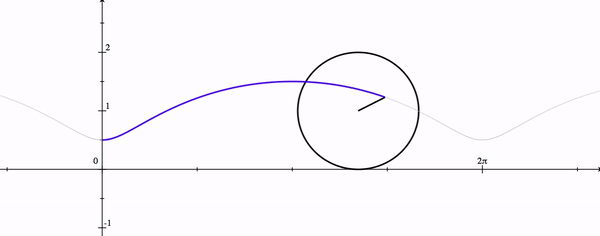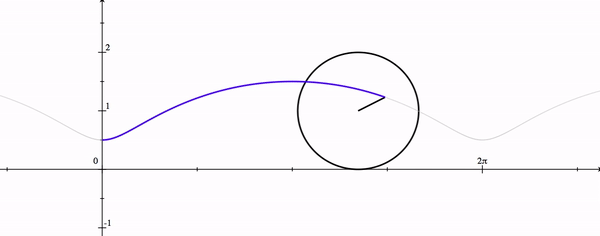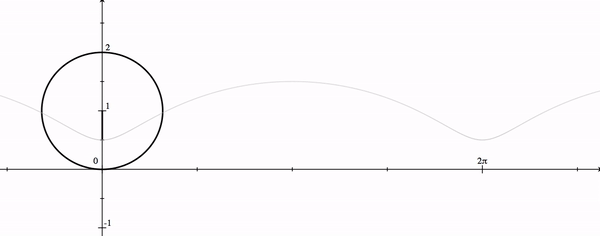
| − | which is half a unit directly below the axle. This is shown as a gray "ghost" dot in the image, while the black triangle and circle represent the situation at <math style="vertical-align: -5px">\theta=\pi/4. </math> | + | which is half a unit directly below the axle. This is shown as a gray "ghost" dot in the image, while the black triangle and circle represent the situation at <math style="vertical-align: -5px">\theta=\pi/4. </math> |
|} | |} | ||
| Line 58: | Line 46: | ||
!Step 3: | !Step 3: | ||
|- | |- | ||
| − | |We therefore have a frame (the axle) that is moving, and a point <math style="vertical-align: 0px">P </math> that is moving relative to the frame. To get the movement relative to the stationary "world", we simply add them up to find | + | |We therefore have a frame (the axle) that is moving, and a point <math style="vertical-align: 0px">P </math> that is moving relative to the frame. To get the movement relative to the stationary "world", we simply add them up to find |
:: <math>P(\theta)\,=\,a(\theta)+p(\theta)\,=\,\left(\theta-\frac{1}{2}\sin\theta,1-\frac{1}{2}\cos\theta\right). </math> | :: <math>P(\theta)\,=\,a(\theta)+p(\theta)\,=\,\left(\theta-\frac{1}{2}\sin\theta,1-\frac{1}{2}\cos\theta\right). </math> | ||
| Line 72: | Line 60: | ||
[[009C_Sample_Final_3|'''<u>Return to Sample Exam</u>''']] | [[009C_Sample_Final_3|'''<u>Return to Sample Exam</u>''']] | ||
<br><br><br> | <br><br><br> | ||
| − | [[File:9CSF3_9Ani_ezgif.gif | | + | [[File:9CSF3_9Ani_ezgif.gif |center|600px]] |
| + | <br> | ||
| + | |||
| + | '''Contributions to this page were made by [[Contributors|John Simanyi]]''' | ||
Latest revision as of 11:52, 19 March 2017
A wheel of radius 1 rolls along a straight line, say the -axis. A point is located halfway between the center of the wheel and the rim. As the wheel rolls, traces a curve. Find parametric equations for the curve.
| Foundations: |
|---|
| Many concepts in physics involve the notion of a relative frame. For example, if I'm in a box dropped from an airplane, I won't be moving relative to the box. However, I'm still heading towards the ground with acceleration Say it drops for 5 seconds, so the box is going when it hits the ground. Even if I jump with all my might and pull off something like of upward velocity, I'll still feel the impact of hitting the ground at
Essentially, equations of motion can often be broken into parts, and then added up. |
Solution:
| Step 1: |
|---|
| If a wheel of radius one is resting at the origin, its axis will be at the point For this solution, we will assume the point is below the axle, although the problem does not state the position of . When the wheel rotates clockwise, it will move to the right. Since the length of the arc defined by an angle on a circle of radius is the wheel will roll forward the length of the arc, which is just
Moreover, the axle's position will change in the same manner, while the height of the axle will always be fixed at . This means we can describe the position of the axle as a function of or |
| Step 2: |
|---|
| Since the wheel is rotating, we also know that our point will rotate around the axle. As described in the problem, it is halfway between the rim and the center/axle, so it is unit away from the axle, and will rotate clockwise. Using our trig relations (while looking at the image), we find that the position of relative to the axle can be described as
Notice that when the point would be at the position which is half a unit directly below the axle. This is shown as a gray "ghost" dot in the image, while the black triangle and circle represent the situation at |
| Step 3: |
|---|
| We therefore have a frame (the axle) that is moving, and a point that is moving relative to the frame. To get the movement relative to the stationary "world", we simply add them up to find
|
| Final Answer: | |
|---|---|
|
|
Contributions to this page were made by John Simanyi