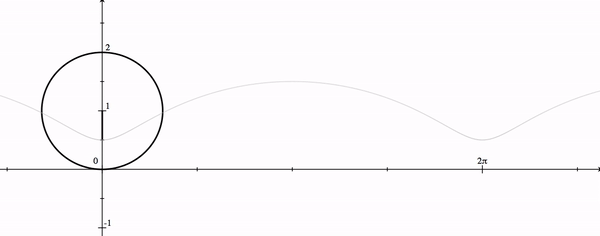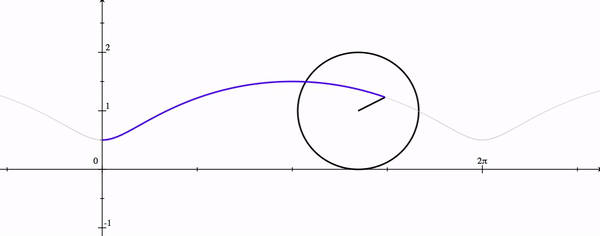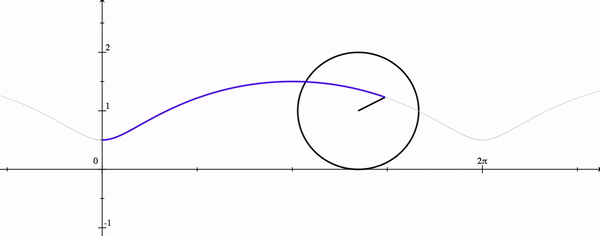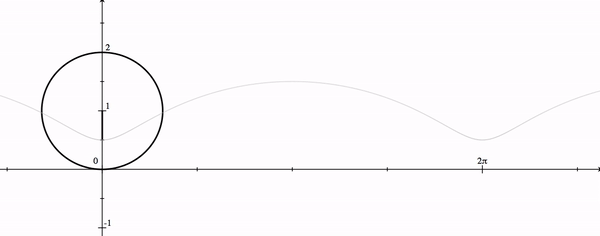
A wheel of radius 1 rolls along a straight line, say the  -axis. A point
-axis. A point  is located halfway between the center of the wheel and the rim. As the wheel rolls,
is located halfway between the center of the wheel and the rim. As the wheel rolls,  traces a curve. Find parametric equations for the curve.
traces a curve. Find parametric equations for the curve.
| ExpandFoundations:
|
Many concepts in physics involve the notion of a relative frame. For example, if I'm in a box dropped from an airplane, I won't be moving relative to the box. However, I'm still heading towards the ground with acceleration  Say it drops for 5 seconds, so the box is going Say it drops for 5 seconds, so the box is going  when it hits the ground. Even if I jump with all my might and pull off something like when it hits the ground. Even if I jump with all my might and pull off something like  of upward velocity, I'll still feel the impact of hitting the ground at of upward velocity, I'll still feel the impact of hitting the ground at

Essentially, equations of motion can often be broken into parts, and
then added up.
|
Solution:
| ExpandStep 1:
|
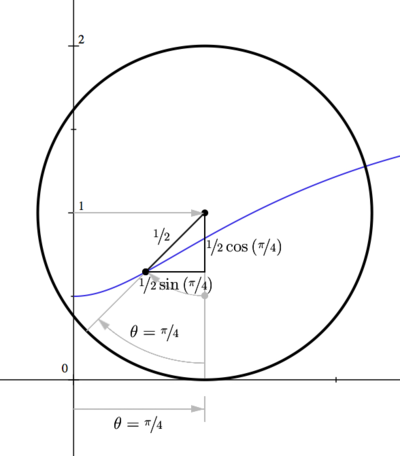
If a wheel of radius one is resting at the origin, its axis will be at the point  For this solution, we will assume the point For this solution, we will assume the point  is below the axle, although the problem does not state the position of is below the axle, although the problem does not state the position of  . When the wheel rotates clockwise, it will move to the right. Since the length of the arc defined by an angle . When the wheel rotates clockwise, it will move to the right. Since the length of the arc defined by an angle  on a circle of radius on a circle of radius  is is  the wheel will roll forward the length of the arc, which is just the wheel will roll forward the length of the arc, which is just 
Moreover, the axle's  position will change in the same manner, while the height of the axle will always be fixed at position will change in the same manner, while the height of the axle will always be fixed at  . This means we can describe the position of the axle as a function of . This means we can describe the position of the axle as a function of  or or

|
| ExpandStep 2:
|
Since the wheel is rotating, we also know that our point  will rotate around the axle. As described in the problem, it is halfway between the rim and the center/axle, so it is will rotate around the axle. As described in the problem, it is halfway between the rim and the center/axle, so it is  unit away from the axle, and will rotate clockwise. Using our trig relations (while looking at the image), we find that the position of unit away from the axle, and will rotate clockwise. Using our trig relations (while looking at the image), we find that the position of  relative to the axle can be described as relative to the axle can be described as

Notice that when  the point would be at the position the point would be at the position

which is half a unit directly below the axle. This is shown as a gray "ghost" dot in the image, while the black triangle and circle represent the situation at 
|
| ExpandStep 3:
|
We therefore have a frame (the axle) that is moving, and a point  that is moving relative to the frame. To get the movement relative to the stationary "world", we simply add them up to find that is moving relative to the frame. To get the movement relative to the stationary "world", we simply add them up to find

|
| ExpandFinal Answer:
|

|
|
Return to Sample Exam
Contributions to this page were made by John Simanyi