Let's say that we want to find the volume of a sphere of radius  using volumes of revolution.
using volumes of revolution.
We know that the equation of a circle of radius  centered at the origin is
centered at the origin is

The upper half semicircle is given by 
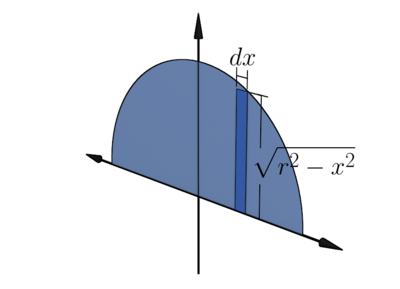
Now, we want to rotate the upper half semicircle around the  -axis. This will give us a sphere of radius
-axis. This will give us a sphere of radius 

We use the washer/disk method to find the volume of the sphere. The volume of the sphere is

Hence, the volume of a sphere of radius  is
is









