Area of a Region Bounded by Two Graphs
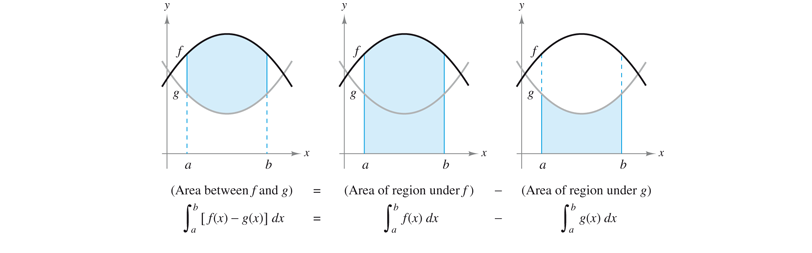
If  and
and  are continuous on
are continuous on ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) and
and  for all
for all  in
in ![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935) ,
then the area of the region bounded by the graphs of
,
then the area of the region bounded by the graphs of  given by
given by
![{\displaystyle A=\int _{a}^{b}[f(x)-g(x)]dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ce99f41c72a8c3bbbb37d5a3bb786ffc5babc0e)
Exercises
1) Find the area of the region bounded by the graph of  and the graph of
and the graph of  .
.
| Solution:
|
Find the bound of the region by setting  , so , so  , hence , hence  , then , then  , therefore , therefore  and and 
|
| Check which function is the top function by choosing one number in between the bound and plug in:
|
Pick  , so , so  , and , and  . Therefore, . Therefore,  will be the top function. will be the top function.
|
![{\displaystyle {\text{Area}}=\int _{0}^{1}[f(x)-g(x)]dx=\int _{0}^{1}[x^{2}-x^{3}]dx=[{\frac {1}{3}}x^{3}-{\frac {1}{4}}x^{4}]{\Biggr |}_{0}^{1}={\frac {1}{3}}(1)^{3}-{\frac {1}{4}}(1)^{4}={\frac {1}{12}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d53527852c97db80cb845d3eb5962d48f34aa86)
|
Consumer Surplus and Producer Surplus
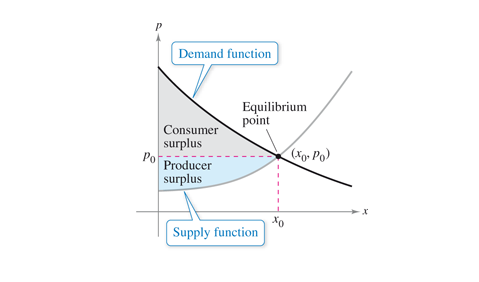
Given the demand function is  and the supply function is
and the supply function is  .
Let
.
Let  be the solution of
be the solution of  .
Then, the Consumer Surplus is
.
Then, the Consumer Surplus is ![{\displaystyle CS=\int _{0}^{x_{0}}[d(x)-p_{0}]dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c52e56aa03070d65a95cad4ee5a630a6874fd831) and the Producer Surplus is
and the Producer Surplus is ![{\displaystyle PS=\int _{0}^{x_{0}}[p_{0}-s(x)]dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3043c15220dda1a6fb17c4e2cc3315e3a84d621a)
Exercises
2) Find the consumer and producer surpluses by using the demand  and supply functions
and supply functions  .
.
| Solution:
|
Find the solution (equilibrium point):  , so , so  , so , so  , then , then  . Therefor, . Therefor,  and and 
|
So ![{\displaystyle CS=\int _{0}^{80}[50-0.5x-10]dx=\int _{0}^{80}[40-0.5x]dx=[40x-{\frac {1}{4}}x^{2}]{\Biggr |}_{0}^{80}=40(80)-{\frac {1}{4}}(80)^{2}=1600}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d63df2fe7d45699c03c9b6c0aca21c04a226f1ab)
|
and ![{\displaystyle PS=\int _{0}^{80}[10-0.125x]dx=[10x-{\frac {0.125}{2}}x^{2}]{\Biggr |}_{0}^{80}=10(80)-{\frac {0.125}{2}}(80^{2})=400}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc64998b740654323faee8099c49fea189009b02)
|
Return to Topics Page
This page were made by Tri Phan



![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)



![{\displaystyle A=\int _{a}^{b}[f(x)-g(x)]dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ce99f41c72a8c3bbbb37d5a3bb786ffc5babc0e)












![{\displaystyle {\text{Area}}=\int _{0}^{1}[f(x)-g(x)]dx=\int _{0}^{1}[x^{2}-x^{3}]dx=[{\frac {1}{3}}x^{3}-{\frac {1}{4}}x^{4}]{\Biggr |}_{0}^{1}={\frac {1}{3}}(1)^{3}-{\frac {1}{4}}(1)^{4}={\frac {1}{12}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d53527852c97db80cb845d3eb5962d48f34aa86)





![{\displaystyle CS=\int _{0}^{x_{0}}[d(x)-p_{0}]dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c52e56aa03070d65a95cad4ee5a630a6874fd831)
![{\displaystyle PS=\int _{0}^{x_{0}}[p_{0}-s(x)]dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3043c15220dda1a6fb17c4e2cc3315e3a84d621a)








![{\displaystyle CS=\int _{0}^{80}[50-0.5x-10]dx=\int _{0}^{80}[40-0.5x]dx=[40x-{\frac {1}{4}}x^{2}]{\Biggr |}_{0}^{80}=40(80)-{\frac {1}{4}}(80)^{2}=1600}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d63df2fe7d45699c03c9b6c0aca21c04a226f1ab)
![{\displaystyle PS=\int _{0}^{80}[10-0.125x]dx=[10x-{\frac {0.125}{2}}x^{2}]{\Biggr |}_{0}^{80}=10(80)-{\frac {0.125}{2}}(80^{2})=400}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc64998b740654323faee8099c49fea189009b02)