009A Sample Midterm 3, Problem 2 Detailed Solution
Jump to navigation
Jump to search
Sketch the graph of At each point of discontinuity, state whether is left or right continuous.
| Background Information: |
|---|
| Suppose is discontinuous at |
| Now, is left continuous at if |
| Similarly, is right continuous at if |
Solution:
| Step 1: |
|---|
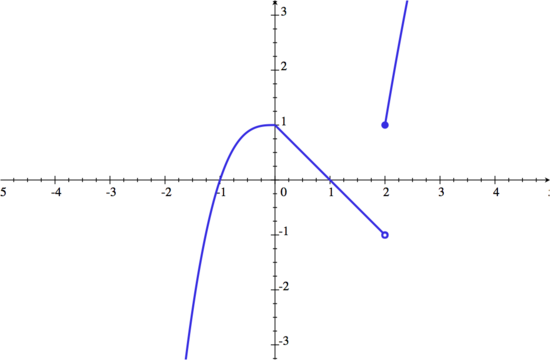
| We start by graphing |
| Step 2: |
|---|
| From the graph, we can see that is discontinuous at |
| Now, we have |
| Hence, is right continuous at |
| Final Answer: |
|---|
| See Step 1 above for graph. |
| is right continuous at |