009C Sample Final 3, Problem 8

A curve is given in polar coordinates by  $r=4+3\sin \theta$

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0\leq \theta \leq 2\pi}

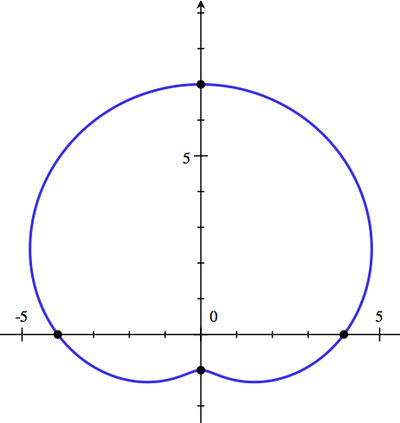
(a) Sketch the curve.

(b) Find the area enclosed by the curve.

Foundations:
The area under a polar curve   Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=f(\theta)}   is given by
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{\alpha_1}^{\alpha_2} \frac{1}{2}r^2~d\theta}   for appropriate values of  Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha_1,\alpha_2.}

Solution:

(a)

(b)

Step 1:
The area enclosed by the curve,  Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A}   is
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} \displaystyle{A} & = & \displaystyle{\int_0^{2\pi} \frac{1}{2}r^2~d\theta}\\ &&\\ & = & \displaystyle{\int_0^{2\pi} \frac{1}{2} (4+3\sin\theta)^2~d\theta.} \end{array}}

Step 2:
Using the double angle formula for  Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \cos(2\theta),}   we have
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} \displaystyle{A} & = & \displaystyle{\frac{1}{2}\int_0^{2\pi} (16+24\sin\theta+9\sin^2\theta)~d\theta} \\ &&\\ & = & \displaystyle{\frac{1}{2}\int_0^{2\pi} \bigg(16+24\sin\theta+\frac{9}{2}(1-\cos(2\theta))\bigg)~d\theta}\\ &&\\ & = & \displaystyle{\frac{1}{2}\bigg[16\theta-24\cos\theta+\frac{9}{2}\theta-\frac{9}{4}\sin(2\theta)\bigg]\bigg|_0^{2\pi}}\\ &&\\ & = & \displaystyle{\frac{1}{2}\bigg[\frac{41}{2}\theta-24\cos\theta-\frac{9}{4}\sin(2\theta)\bigg]\bigg|_0^{2\pi}.}\\ \end{array}}

Step 3:
Lastly, we evaluate to get
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} \displaystyle{A} & = &\displaystyle{\frac{1}{2}\bigg[\frac{41}{2}(2\pi)-24\cos(2\pi)-\frac{9}{4}\sin(4\pi)\bigg]-\frac{1}{2}\bigg[\frac{41}{2}(0)-24\cos(0)-\frac{9}{4}\sin(0)\bigg]}\\ &&\\ & = & \displaystyle{\frac{1}{2}(41\pi-24)-\frac{1}{2}(-24)}\\ &&\\ & = & \displaystyle{\frac{41\pi}{2}.}\\ \end{array}}

Final Answer:
(a)     See above
(b)     Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{41\pi}{2}}

Return to Sample Exam