007A Sample Midterm 2, Problem 4 Detailed Solution

Assume  $N(t)$  denotes the size of a population at time  $t$  and that  $N(t)$  satisfies the equation:

${\frac {dN}{dt}}=3N{\bigg (}1-{\frac {N}{20}}{\bigg )}.$

Let  $f(N)=3N{\bigg (}1-{\frac {N}{20}}{\bigg )},~N\geq 0.$  Graph  $f(N)$  as a function of  $N$  and identify all equilibria. That is, all points where  ${\frac {dN}{dt}}=0.$

---

Background Information:
If  $ab=0,$  then  $a=0$  or  $b=0.$

Solution:

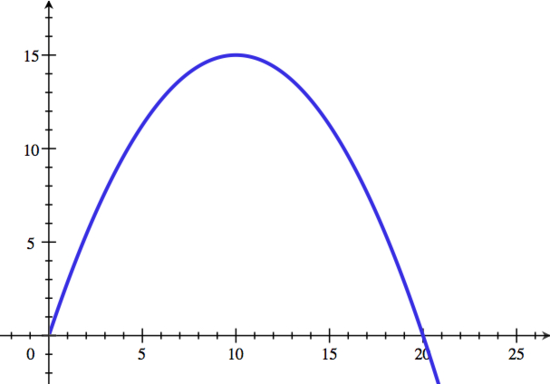
Step 1:
First, we start by graphing  $f(N).$

Step 2:
Now, we want to solve
$0=3N{\bigg (}1-{\frac {N}{20}}{\bigg )}.$
Then, we have  $3N=0$  or  $1-{\frac {N}{20}}=0.$
This means either  $N=0$  or  $N=20.$
Therefore, the equilibria occur at
$N=0$  and  $N=20.$

Final Answer:
See Step 1 for graph
$N=0$  and  $N=20$

Return to Sample Exam