005 Sample Final A, Question 16

Question Graph the following,

$-x^{2}+4y^{2}-2x-16y+11=0$

Foundations:
1) What type of function is this?
2) What can you say about the orientation of the graph?
Answer:
1) Since both x and y are squared it must be a hyperbola or an ellipse. We can conclude that the graph is a hyperbola since $x^{2}$   and   $y^{2}$ have the different signs, one negative and one positive.
2) Since the $y^{2}$ is positive, the hyperbola opens up and down.

Solution:

Step 1:
We start by completing the square twice, once for x and once for y. After completing the squares we end up with $-(x+1)^{2}+4(y-2)^{2}=4$
Common Mistake: When completing the square we will end up adding numbers inside of parenthesis. So make sure you add the correct value to this other side. In this case we add -1, and 16 for completing the square with respect to x and y, respectively.

Step 2:
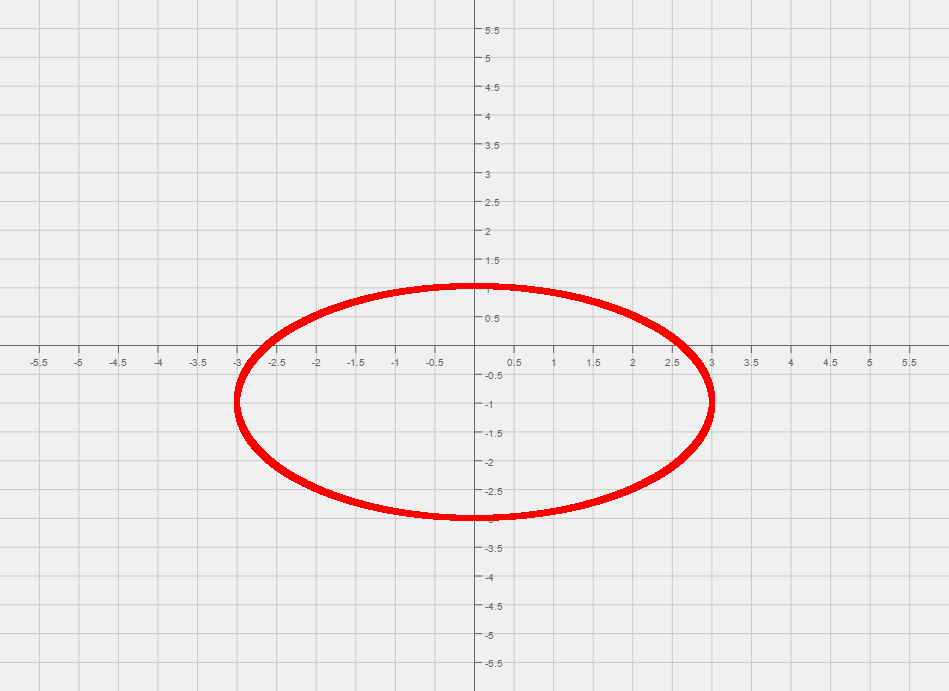
Now that we have the equation that looks like an ellipse, we can read off the center of the ellipse, (0, -1).
From the center mark the two points that are 3 units left, and three units right of the center.
Then mark the two points that are 2 units up, and two units down from the center.

Final Answer:
The four vertices are: $(-3,-1),(3,-1),(0,1){\text{ and }}(0,-3)$

Return to Sample Exam