Volume of a Sphere

Let's say that we want to find the volume of a sphere of radius  $r$  using volumes of revolution.

We know that the equation of a circle of radius  $r$  centered at the origin is

$x^{2}+y^{2}=r^{2}.$

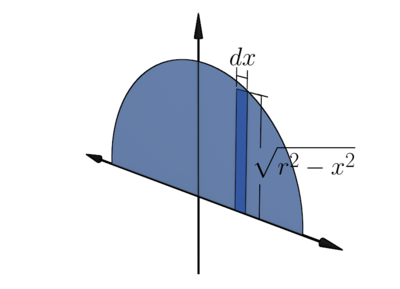
The upper half semicircle is given by  $y={\sqrt {r^{2}-x^{2}}}.$

Now, we want to rotate the upper half semicircle around the  $x$-axis. This will give us a sphere of radius  $r.$

400px

We use the washer/disk method to find the volume of the sphere. The volume of the sphere is

        Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} \displaystyle{V} & = & \displaystyle{\int_{-r}^r \pi (\sqrt{r^2-x^2})^2~dx}\\ &&\\ & = & \displaystyle{\int_{-r}^r \pi (r^2-x^2)~dx}\\ &&\\ & = & \displaystyle{\pi \bigg(r^2x-\frac{x^3}{3}\bigg)\bigg|_{-r}^r}\\ &&\\ & = & \displaystyle{\pi\bigg(r^3-\frac{r^3}{3}\bigg)-\pi\bigg(-r^3+\frac{r^3}{3}\bigg)}\\ &&\\ & = & \displaystyle{\frac{4}{3}\pi r^3.} \end{array}}

Hence, the volume of a sphere of radius  Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r}   is

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V=\frac{4}{3}\pi r^3.}