009A Sample Final 1, Problem 5

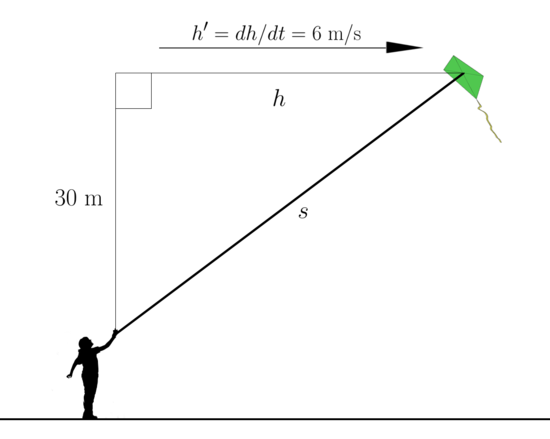
A kite 30 (meters) above the ground moves horizontally at a speed of 6 (m/s). At what rate is the length of the string increasing

when 50 (meters) of the string has been let out?

Foundations:
The Pythagorean Theorem
For a right triangle with side lengths  $a,b,c$  where  $c$  is the length of the
hypotenuse, we have  $a^{2}+b^{2}=c^{2}.$

Solution:

Step 1:
From the diagram, we have  $30^{2}+h^{2}=s^{2}$  by the Pythagorean Theorem.
Taking derivatives, we get
$2hh'=2ss'.$

Step 2:
If   $s=50,$  then
$h={\sqrt {50^{2}-30^{2}}}=40.$
So, we have
$2(40)6=2(50)s'.$
Solving for   $s',$  we get   $s'={\frac {24}{5}}{\text{ m/s.}}$

Final Answer:
$s'={\frac {24}{5}}{\text{ m/s}}$

Return to Sample Exam