009B Sample Midterm 3, Problem 1

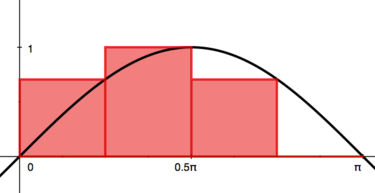
Divide the interval  Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [0,\pi]}   into four subintervals of equal length   Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\pi}{4}}   and compute the right-endpoint Riemann sum of  Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=\sin (x).}

Foundations:
1. The height of each rectangle in the right-hand Riemann sum
is given by choosing the right endpoint of the interval.
2. See the Riemann sums (insert link) for more information.

Solution:

Step 1:
Let  Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)=\sin(x).}
Each interval has length  Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\pi}{4}.}
Therefore, the right-endpoint Riemann sum of  Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)}   on the interval  Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [0,\pi]}   is
${\frac {\pi }{4}}{\bigg (}f{\bigg (}{\frac {\pi }{4}}{\bigg )}+f{\bigg (}{\frac {\pi }{2}}{\bigg )}+f{\bigg (}{\frac {3\pi }{4}}{\bigg )}+f(\pi ){\bigg )}.$

Step 2:
Thus, the right-endpoint Riemann sum is
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} \displaystyle{\frac{\pi}{4}\bigg(\sin\bigg(\frac{\pi}{4}\bigg)+\sin\bigg(\frac{\pi}{2}\bigg)+\sin\bigg(\frac{3\pi}{4}\bigg)+\sin(\pi)\bigg)} & = & \displaystyle{\frac{\pi}{4}\bigg(\frac{\sqrt{2}}{2}+1+\frac{\sqrt{2}}{2}+0\bigg)}\\ &&\\ & = & \displaystyle{\frac{\pi}{4}(\sqrt{2}+1).}\\ \end{array}}

Final Answer:
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\pi}{4}(\sqrt{2}+1)}

Return to Sample Exam