009B Sample Final 1, Problem 1

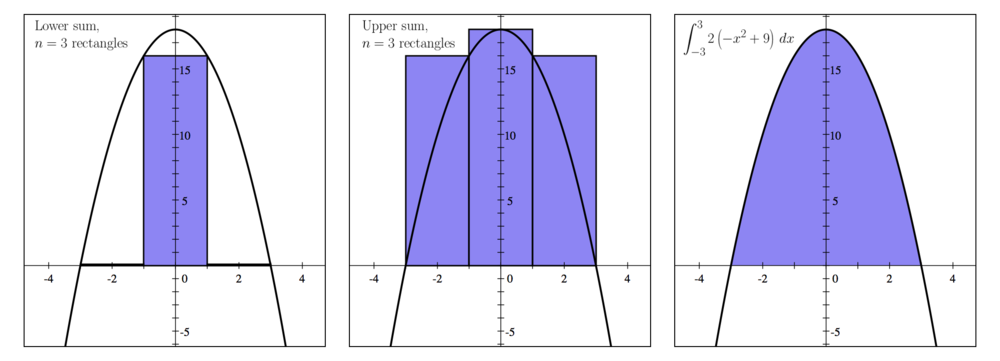
Consider the region bounded by the following two functions:

$y=2(-x^{2}+9)$ and $y=0.$

a) Using the lower sum with three rectangles having equal width, approximate the area.

b) Using the upper sum with three rectangles having equal width, approximate the area.

c) Find the actual area of the region.

Foundations:
Recall:
1. The height of each rectangle in the lower Riemann sum is given by choosing the minimum
$y$ value of the left and right endpoints of the rectangle.
2. The height of each rectangle in the upper Riemann sum is given by choosing the maximum
$y$ value of the left and right endpoints of the rectangle.
3. The area of the region is given by $\int _{a}^{b}y~dx$ for appropriate values $a,b.$

Solution:

(a)

Step 1:
We need to set these two equations equal in order to find the intersection points of these functions.
So, we let
Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle 2(-x^{2}+9)=0.}
Solving for Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle x,} we get Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle x=\pm 3.}
This means that we need to calculate the Riemann sums over the interval Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle [-3,3].}

Step 2:
Since the length of our interval is $6$ and we are using $3$ rectangles,
each rectangle will have width $2.$
Thus, the lower Riemann sum is
Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle 2(f(-3)+f(-1)+f(3))\,=\,2(0+16+0)\,=\,32.}

(b)

Step 1:
As in Part (a), the length of our inteval is $6$ and
each rectangle will have width $2.$ (See Step 1 and 2 for (a))

Step 2:
Thus, the upper Riemann sum is
Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle 2(f(-1)+f(-1)+f(1))\,=\,2(16+16+16)\,=\,96.}

(c)

Step 1:
To find the actual area of the region, we need to calculate
Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle \int _{-3}^{3}2(-x^{2}+9)~dx.}

Step 2:
We integrate to get
${\begin{array}{rcl}\displaystyle {\int _{-3}^{3}2(-x^{2}+9)~dx}&=&\displaystyle {2{\bigg (}{\frac {-x^{3}}{3}}+9x{\bigg )}{\bigg |}_{-3}^{3}}\\&&\\&=&\displaystyle {2{\bigg (}{\frac {-3^{3}}{3}}+9\times 3{\bigg )}-2{\bigg (}{\frac {-(-3)^{3}}{3}}+9(-3){\bigg )}}\\&&\\&=&\displaystyle {2(-9+27)-2(9-27)}\\&&\\&=&\displaystyle {2(18)-2(-18)}\\&&\\&=&\displaystyle {72}.\\\end{array}}$

Final Answer:
(a)  $32$
(b)  Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle 96}
(c)  Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. Server problem."): {\displaystyle 72}

Return to Sample Exam