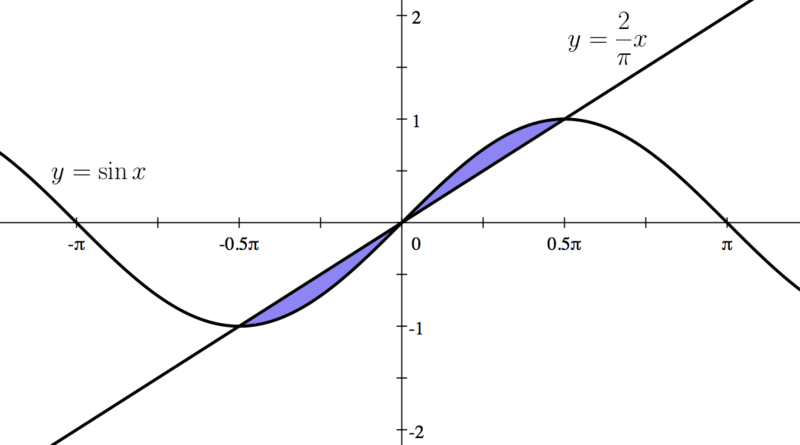
Consider the area bounded by the following two functions:
 and
and 
- a) Find the three intersection points of the two given functions. (Drawing may be helpful.)
- b) Find the area bounded by the two functions.
| Foundations:
|
| Recall:
|
- 1. You can find the intersection points of two functions, say

|
- by setting
 and solving for and solving for 
|
- 2. The area between two functions,
 and and  is given by is given by 
|
- for
 where where  is the upper function and is the upper function and  is the lower function. is the lower function.
|
Solution:
(a)
| Step 1:
|
| First, we graph these two functions.
|
|
|
| Step 2:
|
Setting  we get three solutions: we get three solutions:
|

|
So, the three intersection points are 
|
| You can see these intersection points on the graph shown in Step 1.
|
(b)
| Step 1:
|
| Using symmetry of the graph, the area bounded by the two functions is given by
|

|
|
|
| Step 2:
|
| Lastly, we integrate to get
|

|
| Final Answer:
|
(a) 
|
(b) 
|
Return to Sample Exam