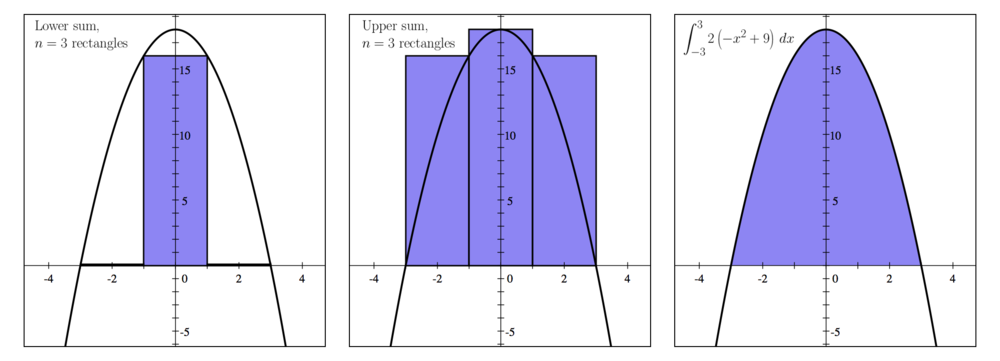
Consider the region bounded by the following two functions:
-
 and
and 
- a) Using the lower sum with three rectangles having equal width, approximate the area.
- b) Using the upper sum with three rectangles having equal width, approximate the area.
- c) Find the actual area of the region.
| Foundations:
|
| Recall:
|
1. The height of each rectangle in the lower Riemann sum is given by choosing the minimum  value of the left and right endpoints of the rectangle. value of the left and right endpoints of the rectangle.
|
2. The height of each rectangle in the upper Riemann sum is given by choosing the maximum  value of the left and right endpoints of the rectangle. value of the left and right endpoints of the rectangle.
|
3. The area of the region is given by  for appropriate values for appropriate values  . .
|
Solution:
(a)
| Step 1:
|
| We need to set these two equations equal in order to find the intersection points of these functions.
|
So, we let  . Solving for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x}
, we get Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=\pm 3}
. . Solving for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x}
, we get Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=\pm 3}
.
|
| This means that we need to calculate the Riemann sums over the interval Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle [-3,3]}
.
|
|
|
| Step 2:
|
| Since the length of our interval is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 6}
and we are using Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 3}
rectangles,
|
| each rectangle will have width Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2}
.
|
| Thus, the lower Riemann sum is
|
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2(f(-3)+f(-1)+f(3))\,=\,2(0+16+0)\,=\,32.}
|
(b)
| Step 1:
|
| As in Part (a), the length of our inteval is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 6}
and
|
| each rectangle will have width Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2}
. (See Step 1 and 2 for (a))
|
| Step 2:
|
| Thus, the upper Riemann sum is
|
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2(f(-1)+f(-1)+f(1))\,=\,2(16+16+16)\,=\,96.}
|
(c)
| Step 1:
|
| To find the actual area of the region, we need to calculate
|
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_{-3}^3 2(-x^2+9)~dx.}
|
| Step 2:
|
| We integrate to get
|
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} \displaystyle{\int_{-3}^3 2(-x^2+9)~dx} & = & \displaystyle{2\bigg(\frac{-x^3}{3}+9x\bigg)\bigg|_{-3}^3}\\ &&\\ & = & \displaystyle{2\bigg(\frac{-3^3}{3}+9\times 3\bigg)-2\bigg(\frac{-(-3)^3}{3}+9(-3)\bigg)}\\ &&\\ & = & \displaystyle{2(-9+27)-2(9-27)}\\ &&\\ & = & \displaystyle{2(18)-2(-18)}\\ &&\\ & = & \displaystyle{72}.\\ \end{array}}
|
| Final Answer:
|
| (a) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 32}
|
| (b) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 96}
|
| (c) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 72}
|
Return to Sample Exam