Prototype Calculus Question

Find the volume of the solid obtained by rotating the area enclosed by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=5-x } and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=25-x^2 }
around the x-axis.

Foundations
• Choose either shell or washer method.
• Find the appropriate radii.
• Determine the bounds of integration by finding when both functions have the same y value.
• Using the determined values, set up and solve the integral.

Solution:

Step 1:
Choosing the Approach:   Since we are rotating around the x-axis, the washer method would utilize tall rectangles with dx as their width. This seems like a reasonable choice, as these rectangles would be trapped between our two functions as x varies over the enclosed region, allowing us to solve a single integral. Note that the washer method will require an inner and outer radius, as well as bounds of integration, in order to solve evaluate the integral
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V=\pi \int_{x_1}^{\, x_2} R^2-r^2 \,dx}

Step 2:
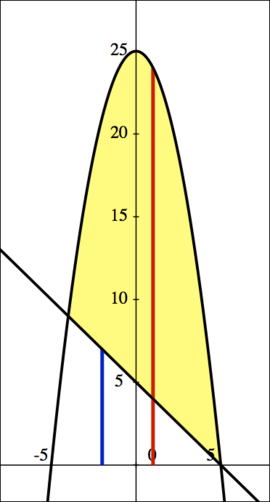
Finding the Radii:  Since our rectangles will be trapped between the two functions, and will be rotated around the x-axis (where y = 0), we find
the inner radius is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r = 5-x } , represented by the blue line, while
the outer radius is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle R = 25-x^2 } , represented by the red line.

Step 3:
Finding the Bounds of Integration:   We must set the two functions equal, and solve. If
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 5-x=25-x^2,}
then by moving all terms to the left hand side and factoring,
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2-x-20=(x+4)(x-5)=0,}
so we have -4 and 5 as solutions. These are our bounds of integration.

Step 4:
Evaluating the Integral:   Using the earlier steps, we have
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle V=\pi \int_{x_1}^{\, x_2} R^2-r^2 \,dx}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\pi \int_{-4}^{\, 5} (25-x^2)^2-(5-x)^2 \,dx}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\pi \int_{-4}^{\, 5} 625-50x^2+x^4-(25-10x+x^2) \,dx}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\pi \int_{-4}^{\, 5} 600-51x^2+x^4+10x \,dx}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\pi \int_{-4}^{\, 5} 600-51x^2+x^4+10x \,dx}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\pi \biggr(600x-51\cdot\frac{x^{3}}{3}+\frac{x^{5}}{5}+10\cdot\frac{x^{2}}{2}\biggr)\biggr|_{x=-4}^{5}}
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle =\frac{15,309}{5} \,\pi.}