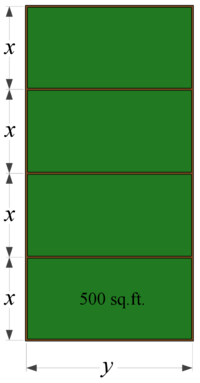
7. A farmer wishes to make 4 identical rectangular pens, each with
500 sq. ft. of area. What dimensions for each pen will use the least
amount of total fencing?
| Foundations:
|
| As a word problem, we must begin by assigning variables in order to construct useful equation(s). As an optimization problem, we will be taking a derivative of one of our equations in order to find an extreme point.
|
Solution:
| Step 1:
|
| Declare Variables: We are attempting to find the dimensions of a single pen, such that we use as little fencing as possible for all four pens. Let's use x and y as indicated in the image, and simply call the length of fencing required L.
|
| Step 2:
|
| Form the Equations: Notice that we need fencing between each of the pens (think "lion-antelope-lion-antelope" if this isn't clear). We require 2 pieces of length x for each pen, and a total of 5 pieces of length y. Together, we need a total length of L = 8x + 5y.
|
| On the other hand, we know that each pen has a fixed area of 500 square feet. Thus, we also know that xy = 500.
|
| Step 3:
|
| Optimize: Since xy = 500, we also know y = 500/x. Plugging this into our equation for length, we have
|
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L(x) = 8x + 5\cdot \frac{500}{x} = 8x + \frac{2500}{x}.}
|
| We now take the derivative to find
|
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L'(x)=8-\frac{2500}{x^2}= \frac{8x^2-2500}{x^2}.}
|
| The denominator can never be zero, and if we set the numerator to zero we find
|
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=\pm\sqrt{\frac{2500}{8}} = \pm\frac{50}{2\sqrt{2}} =\pm\frac{\,\,25}{\sqrt{2}}.}
|
| Of course, we can't have negative fencing lengths, so we can ignore the negative root. Finally, we use the area relation to find
|

|
| Thus, the least amount of fencing is used when we size our 500 sq. ft. pens as 20√2 feet by 25/√2 feet.
|
Return to Sample Exam