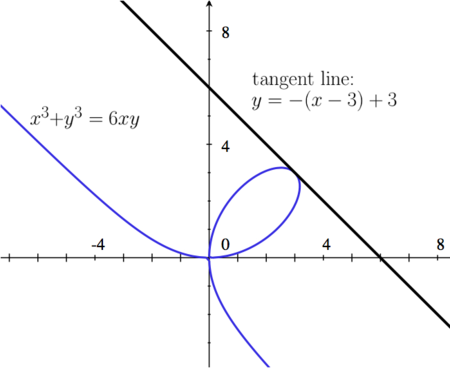
A curve is defined implicitly by the equation

- a) Using implicit differentiation, compute
 .
.
- b) Find an equation of the tangent line to the curve
 at the point
at the point  .
.
| Foundations:
|
1. What is the result of implicit differentiation of 
|
- It would be
 by the Product Rule. by the Product Rule.
|
| 2. What two pieces of information do you need to write the equation of a line?
|
- You need the slope of the line and a point on the line.
|
| 3. What is the slope of the tangent line of a curve?
|
- The slope is

|
Solution:
(a)
| Step 1:
|
Using implicit differentiation on the equation  we get we get
|

|
| Step 2:
|
Now, we move all the  terms to one side of the equation. terms to one side of the equation.
|
| So, we have
|

|
| We solve to get
|

|
(b)
| Step 1:
|
First, we find the slope of the tangent line at the point 
|
We plug  into the formula for into the formula for  we found in part (a). we found in part (a).
|
| So, we get
|

|
| Step 2:
|
Now, we have the slope of the tangent line at  and a point. and a point.
|
| Thus, we can write the equation of the line.
|
So, the equation of the tangent line at  is is
|

|
|
|
| Final Answer:
|
(a) 
|
(b) 
|
Return to Sample Exam