009A Sample Final A, Problem 9
Jump to navigation
Jump to search
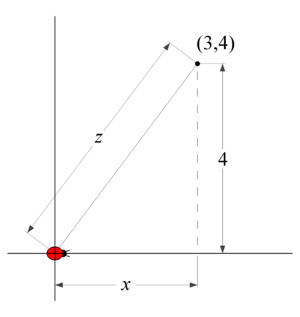
9. A bug is crawling along the -axis at a constant speed of .
How fast is the distance between the bug and the point changing
when the bug is at the origin? (Note that if the distance is decreasing, then you should have a negative answer).
| Foundations: |
|---|
| Like most geometric word problems, you should start with a picture. This will help you declare variables and write meaningful equation(s). In this case, we will have to use implicit differentiation to arrive at our related rate. |
Solution:
| Part (a): |
|---|
| We need to find two values a and b such that one is positive, and one is negative. Notice that f(0) = √2, which is greater than zero. We can choose x = -1, to find f(-1) = -2 - 4 + √2, which is less than zero. Since f is clearly continuous, the IVT tells us there exists a c between -1 and 0 such that f(c) = 0. |