004 Sample Final A, Problem 4

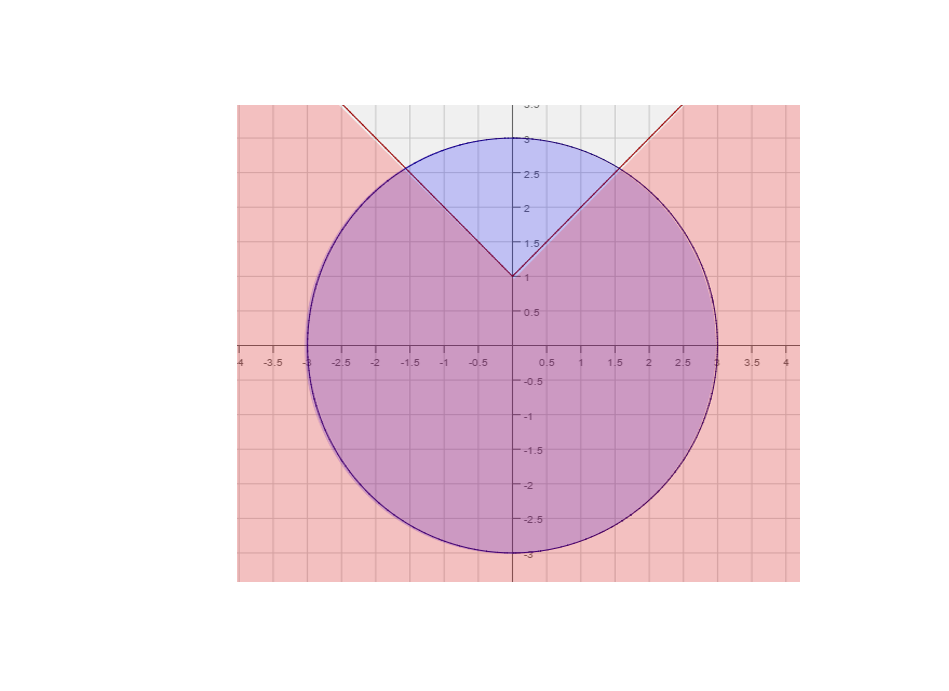
Graph the system of inequalities. $y>2x-3\qquad y\leq 4-x^{2}$ Solution:

Step 1:
First we replace the inequalities with equality. So $y=\vert x\vert +1$, and $x^{2}+y^{2}=9$.
Now we graph both functions.

Step 2:
Now that we have graphed both functions we need to know which region to shade with respect to each graph.
To do this we pick a point an equation and a point not on the graph of that equation. We then check if the
point satisfies the inequality or not. For both equations we will pick the origin.
$y<\vert x\vert +1:$ Plugging in the origin we get, $0<\vert 0\vert +1=1$. Since the inequality is satisfied shade the side of
$y<\vert x\vert +1$ that includes the origin. We make the graph of $y<\vert x\vert +1$, since the inequality is strict.
$x^{2}+y^{2}\leq 9:$ $(0)^{2}+(0)^{2}=0\leq 9$. Once again the inequality is satisfied. So we shade the inside of the circle.
We also shade the boundary of the circle since the inequality is $\leq$

Final Answer:
The final solution is the portion of the graph that below $y=\vert x\vert +1$ and inside $x^{2}+y^{2}=9$
The region we are referring to is shaded both blue and red.

Return to Sample Exam