008A Sample Final A, Question 6

Question: Sketch $4x^{2}+9(y+1)^{2}=36$. Give coordinates of each of the 4 vertices of the graph.

Foundations
1) What type of function is this?
2) What can you say about the orientation of the graph?
Answer:
1) Since both x and y are squared it must be a hyperbola or an ellipse. Since the coefficients of the $x^{2}$ and $y^{2}$ terms are both positive the graph must be an ellipse.
2) Since the coefficient of the $x^{2}$ term is smaller, when we divide both sides by 36 the X-axis will be the major axis.

Solution:

Step 1:
We start by dividing both sides by 36. This yields Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{4x^2}{36} + \frac{9(y + 1)^2}{36} = \frac{x^2}{9} + \frac{(y+1)^2}{4} = 1} .

Step 2:
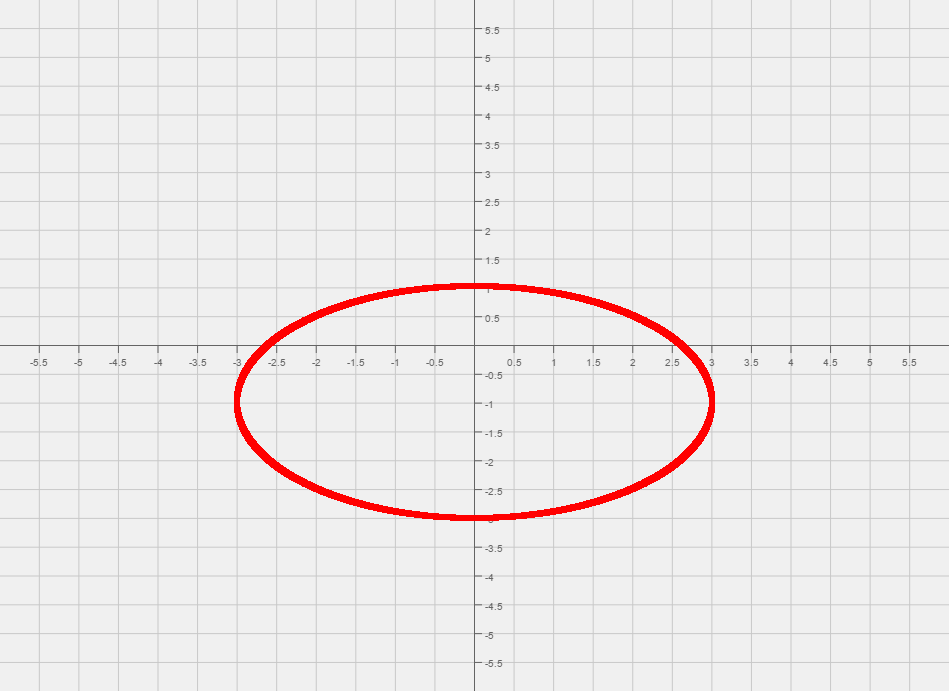
Now that we have the equation that looks like an ellipse, we can read off the center of the ellipse, (0, -1).
From the center mark the two points that are 3 units left, and three units right of the center.
Then mark the two points that are 2 units up, and two units down from the center.

Final Answer:

Return to Sample Exam