009A Sample Midterm 2, Problem 1
Evaluate the following limits.
(a) Find
(b) Find
(c) Evaluate Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim _{x\rightarrow (\frac{\pi}{2})^-} \tan(x) }
| Foundations: |
|---|
| Recall |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim_{x\rightarrow 0} \frac{\sin x}{x}=1} |
Solution:
(a)
| Step 1: |
|---|
| We begin by noticing that if we plug in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=2} into |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\sqrt{x^2+12}-4}{x-2},} |
| we get Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{0}{0}.} |
| Step 2: |
|---|
| Now, we multiply the numerator and denominator by the conjugate of the numerator. |
| Hence, we have |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} \displaystyle{\lim _{x\rightarrow 2} \frac{\sqrt{x^2+12}-4}{x-2}} & = & \displaystyle{\lim_{x\rightarrow 2} \frac{(\sqrt{x^2+12}-4)}{(x-2)}\frac{(\sqrt{x^2+12}+4)}{(\sqrt{x^2+12}+4)}}\\ &&\\ & = & \displaystyle{\lim_{x\rightarrow 2} \frac{(x^2+12)-16}{(x-2)(\sqrt{x^2+12}+4)}}\\ &&\\ & = & \displaystyle{\lim_{x\rightarrow 2} \frac{x^2-4}{(x-2)(\sqrt{x^2+12}+4)}}\\ &&\\ & = & \displaystyle{\lim_{x\rightarrow 2} \frac{(x-2)(x+2)}{(x-2)(\sqrt{x^2+12}+4)}}\\ &&\\ & = & \displaystyle{\lim_{x\rightarrow 2} \frac{x+2}{\sqrt{x^2+12}+4}}\\ &&\\ & = & \displaystyle{\frac{4}{8}}\\ &&\\ & = & \displaystyle{\frac{1}{2}.} \end{array}} |
(b)
| Step 1: |
|---|
| First, we write |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} \displaystyle{\lim_{x\rightarrow 0} \frac{\sin(3x)}{\sin(7x)}} & = & \displaystyle{\lim_{x\rightarrow 0} \frac{\sin(3x)}{x} \frac{x}{\sin(7x)}}\\ &&\\ & = & \displaystyle{\lim_{x\rightarrow 0} \frac{3}{7} \frac{\sin(3x)}{3x}\frac{7x}{\sin(7x)}}\\ &&\\ & = & \displaystyle{\frac{3}{7}\lim_{x\rightarrow 0} \frac{\sin(3x)}{3x}\frac{7x}{\sin(7x)}.} \end{array}} |
| Step 2: |
|---|
| Now, we have |
|
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{array}{rcl} \displaystyle{\lim_{x\rightarrow 0} \frac{\sin(3x)}{\sin(7x)}} & = & \displaystyle{\frac{3}{7}\lim_{x\rightarrow 0} \frac{\sin(3x)}{3x}\frac{7x}{\sin(7x)}}\\ &&\\ & = & \displaystyle{\frac{3}{7}\bigg(\lim_{x\rightarrow 0} \frac{\sin(3x)}{3x}\bigg)\bigg(\lim_{x\rightarrow 0} \frac{7x}{\sin(7x)}\bigg)}\\ &&\\ & = & \displaystyle{\frac{3}{7} (1)(1)}\\ &&\\ & = & \displaystyle{\frac{3}{7}.} \end{array}} |
(c)
| Step 1: |
|---|
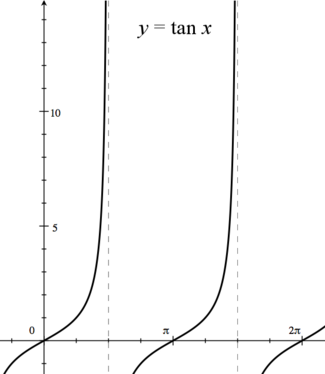
| We begin by looking at the graph of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=\tan(x),} |
| which is displayed below. |
| Step 2: |
|---|
| We are taking a left hand limit. So, we approach Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=\frac{\pi}{2}} from the left. |
| If we look at the graph from the left of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=\frac{\pi}{2}} and go towards Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{\pi}{2},} |
| we see that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tan(x)} goes to Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \infty.} |
| Therefore, |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \lim _{x\rightarrow (\frac{\pi}{2})^-} \tan(x)=\infty.} |
| Final Answer: |
|---|
| (a) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{1}{2}} |
| (b) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{3}{7}} |
| (c) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \infty} |