A curve is given in polar parametrically by
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y(t)=4\cos t}
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0\leq t \leq 2\pi}
- a) Sketch the curve.
- b) Compute the equation of the tangent line at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_0=\frac{\pi}{4}}
.
| Foundations:
|
| 1. What two pieces of information do you need to write the equation of a line?
|
- You need the slope of the line and a point on the line.
|
| 2. What is the slope of the tangent line of a parametric curve?
|
- The slope is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m=\frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}.}
|
Solution:
(a)
| Step 1:
|
|
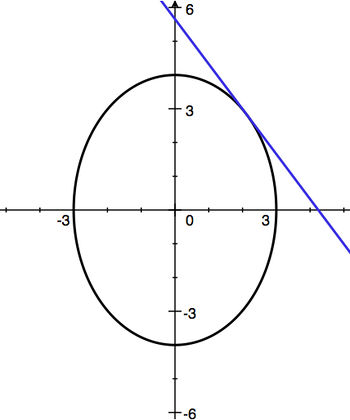
(b)
| Step 1:
|
| First, we need to find the slope of the tangent line.
|
| Since Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dy}{dt}=-4\sin t}
and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dx}{dt}=3\cos t,}
we have
|
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}=\frac{-4\sin t}{3\cos t}.}
|
| So, at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_0=\frac{\pi}{4},}
the slope of the tangent line is
|
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle m=\frac{-4\sin\bigg(\frac{\pi}{4}\bigg)}{3\cos\bigg(\frac{\pi}{4}\bigg)}=\frac{-4}{3}.}
|
| Step 2:
|
| Since we have the slope of the tangent line, we just need a find a point on the line in order to write the equation.
|
| If we plug in Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_0=\frac{\pi}{4}}
into the equations for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x(t)}
and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y(t),}
we get
|
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x\bigg(\frac{\pi}{4}\bigg)=3\sin\bigg(\frac{\pi}{4}\bigg)=\frac{3\sqrt{2}}{2}}
and
|
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y\bigg(\frac{\pi}{4}\bigg)=4\cos\bigg(\frac{\pi}{4}\bigg)=2\sqrt{2}.}
|
| Thus, the point Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \bigg(\frac{3\sqrt{2}}{2},2\sqrt{2}\bigg)}
is on the tangent line.
|
| Step 3:
|
| Using the point found in Step 2, the equation of the tangent line at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle t_0=\frac{\pi}{4}}
is
|
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=\frac{-4}{3}\bigg(x-\frac{3\sqrt{2}}{2}\bigg)+2\sqrt{2}.}
|
| Final Answer:
|
| (a) See Step 1 above for the graph.
|
| (b) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=\frac{-4}{3}\bigg(x-\frac{3\sqrt{2}}{2}\bigg)+2\sqrt{2}}
|
Return to Sample Exam
