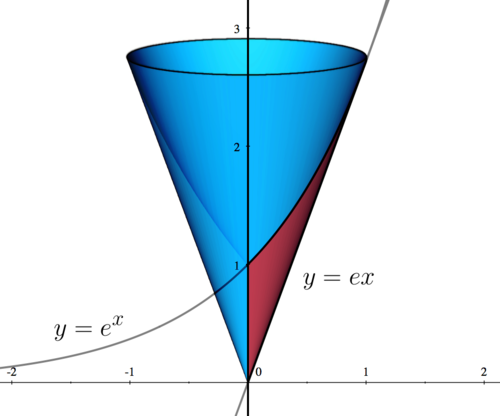
Consider the solid obtained by rotating the area bounded by the following three functions about the  -axis:
-axis:
-
 ,
,  , and
, and  .
.
- a) Sketch the region bounded by the given three functions. Find the intersection point of the two functions:
 and
and  . (There is only one.)
. (There is only one.)
- b) Set up the integral for the volume of the solid.
- c) Find the volume of the solid by computing the integral.
| Foundations:
|
| Recall:
|
- 1. You can find the intersection points of two functions, say

|
- by setting
 and solving for and solving for 
|
- 2. The volume of a solid obtained by rotating an area around the
 -axis using cylindrical shells is given by -axis using cylindrical shells is given by
|
 where where  is the radius of the shells and is the radius of the shells and  is the height of the shells. is the height of the shells.
|
Solution:
(a)
| Step 1:
|
| First, we sketch the region bounded by the three functions. The region is shown in red, while the revolved solid is shown in blue.
|
|
|
|
|
| Step 2:
|
Setting the equations equal, we have 
|
We get one intersection point, which is 
|
| This intersection point can be seen in the graph shown in Step 1.
|
(b)
| Step 1:
|
We proceed using cylindrical shells. The radius of the shells is given by 
|
| The height of the shells is given by
|

|
| Step 2:
|
| So, the volume of the solid is
|

|
(c)
| Step 1:
|
| We need to integrate
|

|
| Step 2:
|
| For the first integral, we need to use integration by parts.
|
Let  and and  Then, Then,  and and 
|
| So, the integral becomes
|

|
| Final Answer:
|
(a)  (See Step 1 for the graph) (See Step 1 for the graph)
|
(b) 
|
(c) 
|
Return to Sample Exam