Difference between revisions of "008A Sample Final A, Question 5"
Jump to navigation
Jump to search
(Created page with "'''Question: '''Graph the system of inequalities <math>y < \vert x\vert +1 </math> <math>x^2 + y^2 \le 9</math> {| class="mw-collapsible mw...") |
|||
| Line 54: | Line 54: | ||
|- | |- | ||
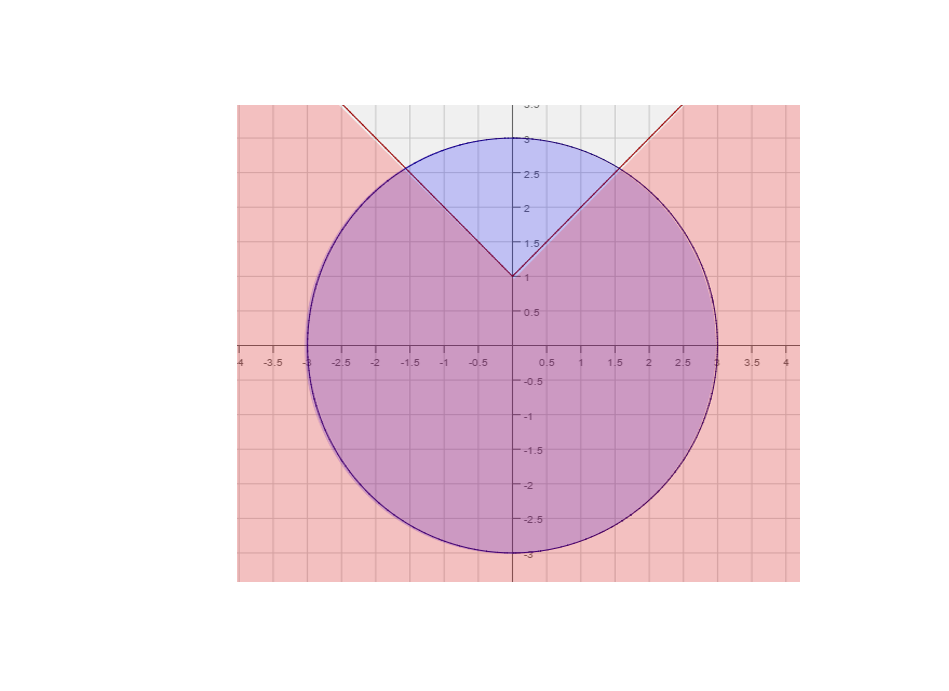
|The final solution is the portion of the graph that below <math>y = \vert x\vert + 1</math> and inside <math> x^2 + y^2 = 9</math> | |The final solution is the portion of the graph that below <math>y = \vert x\vert + 1</math> and inside <math> x^2 + y^2 = 9</math> | ||
| + | |[[File:8A_Final_5.png]] | ||
|} | |} | ||
[[008A Sample Final A|<u>'''Return to Sample Exam</u>''']] | [[008A Sample Final A|<u>'''Return to Sample Exam</u>''']] | ||
Revision as of 13:44, 28 April 2015
Question: Graph the system of inequalities
| Foundations |
|---|
| 1) What do the graphs of , and look like? |
| 2) Each graph splits the plane into two regions. Which one do you want to shade? |
| Answer: |
| 1) The first graph looks like a V with the vertex at (0, 1), the latter is a circle centered at the origin with radius 3. |
| 2) Since the Y-value must be less than , shade below the V. For the circle shde the inside. |
Solution:
| Step 1: |
|---|
| First we replace the inequalities with equality. So , and . |
| Now we graph both functions. |
| Step 2: |
|---|
| Now that we have graphed both functions we need to know which region to shade with respect to each graph. |
| To do this we pick a point an equation and a point not on the graph of that equation. We then check if the |
| point satisfies the inequality or not. For both equations we will pick the origin. |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y < \vert x\vert + 1:} Plugging in the origin we get, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 0 < \vert 0\vert + 1 = 1} . Since the inequality is satisfied shade the side of |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y < \vert x\vert + 1} that includes the origin. We make the graph of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y < \vert x\vert + 1} , since the inequality is strict. |
| Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2 + y^2 \le 9:} Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (0)^2 +(0)^2 = 0 \le 9} . Once again the inequality is satisfied. So we shade the inside of the circle. |
| We also shade the boundary of the circle since the inequality is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \le} |
| Step 3: |
|---|
| The final solution is the portion of the graph that below Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y = \vert x\vert + 1} and inside Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^2 + y^2 = 9} |