Difference between revisions of "009B Sample Final 1, Problem 1"
Jump to navigation
Jump to search
| Line 113: | Line 113: | ||
!Final Answer: | !Final Answer: | ||
|- | |- | ||
| − | |'''(a)''' <math style="vertical-align: 0px">32</math> | + | | '''(a)''' <math style="vertical-align: 0px">32</math> |
|- | |- | ||
| − | |'''(b)''' <math style="vertical-align: 0px">96</math> | + | | '''(b)''' <math style="vertical-align: 0px">96</math> |
|- | |- | ||
| − | |'''(c)''' <math style="vertical-align: 0px">72</math> | + | | '''(c)''' <math style="vertical-align: 0px">72</math> |
|} | |} | ||
[[009B_Sample_Final_1|'''<u>Return to Sample Exam</u>''']] | [[009B_Sample_Final_1|'''<u>Return to Sample Exam</u>''']] | ||
[[File:9BF1 1 GP.png|center|1000px]] | [[File:9BF1 1 GP.png|center|1000px]] | ||
Revision as of 14:09, 18 April 2016
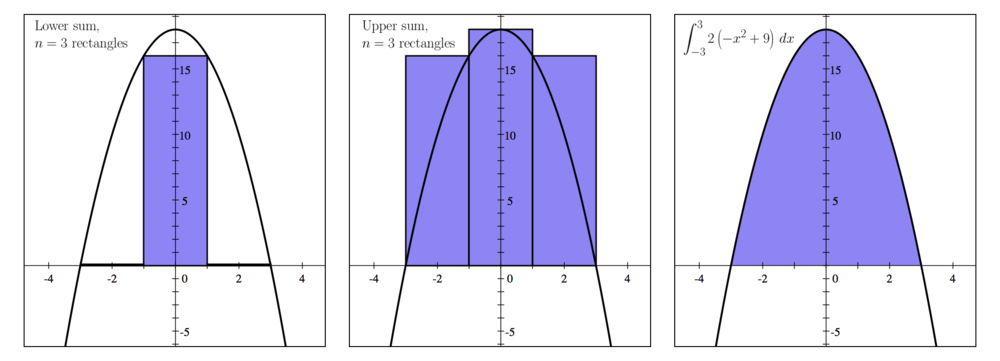
Consider the region bounded by the following two functions:
- and
- a) Using the lower sum with three rectangles having equal width, approximate the area.
- b) Using the upper sum with three rectangles having equal width, approximate the area.
- c) Find the actual area of the region.
| Foundations: |
|---|
| Recall: |
|
|
|
|
|
Solution:
(a)
| Step 1: |
|---|
| We need to set these two equations equal in order to find the intersection points of these functions. |
| So, we let |
|
|
| Solving for we get |
| This means that we need to calculate the Riemann sums over the interval |
| Step 2: |
|---|
| Since the length of our interval is and we are using rectangles, |
| each rectangle will have width |
| Thus, the lower Riemann sum is |
|
|
(b)
| Step 1: |
|---|
| As in Part (a), the length of our inteval is and |
| each rectangle will have width (See Step 1 and 2 for (a)) |
| Step 2: |
|---|
| Thus, the upper Riemann sum is |
|
|
(c)
| Step 1: |
|---|
| To find the actual area of the region, we need to calculate |
|
|
| Step 2: |
|---|
| We integrate to get |
|
|
| Final Answer: |
|---|
| (a) |
| (b) |
| (c) |








![{\displaystyle [-3,3].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2fd4965b1b60b2cd619e047375423a5fbe2d03a)