Difference between revisions of "009A Sample Final A, Problem 9"

From Math Wiki
Jump to navigation Jump to search
Line 9: Line 9:
 
! Foundations:    
 
! Foundations:    
 
|-
 
|-
−
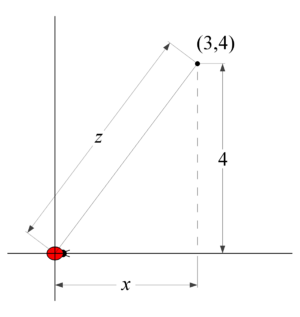
|Like most geometric word problems, you should start with a picture.  This will help you declare variables and write meaningful equation(s). In this case, we will have to use implicit differentiation to arrive at our related rate.
+
|Like most geometric word problems, you should start with a picture.  This will help you declare variables and write meaningful equation(s). In this case, we will have to use implicit differentiation to arrive at our related rate. In particular, we need to choose variables to describe the distance between the bug and the point (3,4), which we can call ''z''.  By the given information, we can consider the position on the ''x''-axis simply as ''x''.
 
|}
 
|}
 
'''Solution:'''
 
'''Solution:'''
  
 
{| class="mw-collapsible mw-collapsed" style = "text-align:left;"
 
{| class="mw-collapsible mw-collapsed" style = "text-align:left;"
−
!Part (a):  
+
!Step 1:  
 
|-
 
|-
−
|We need to find two values ''a'' and ''b'' such that one is positive, and one is negative.  Notice that ''f''(0) = &radic;<span style="text-decoration:overline">2</span>, which is greater than zero.<br>We can choose ''x'' = -1, to find ''f''(-1) = -2 - 4 + &radic;<span style="text-decoration:overline">2</span>, which is less than zero.  Since ''f'' is clearly continuous, the IVT tells us there exists a ''c'' between -1 and 0 such that ''f''(''c'') = 0.
+
|'''Write the Basic Equation:'''From the picture, we can see there is a triangle involving both the bug and the point (3,4).  From this, we can see that <math style="vertical-align: 0%;">z^2 = x^2 +4^2.</math>
 
|}
 
|}

Revision as of 21:41, 23 March 2015

BugGP.png

9. A bug is crawling along the -axis at a constant speed of   . How fast is the distance between the bug and the point changing when the bug is at the origin? (Note that if the distance is decreasing, then you should have a negative answer).

Foundations:  
Like most geometric word problems, you should start with a picture. This will help you declare variables and write meaningful equation(s). In this case, we will have to use implicit differentiation to arrive at our related rate. In particular, we need to choose variables to describe the distance between the bug and the point (3,4), which we can call z. By the given information, we can consider the position on the x-axis simply as x.

Solution:

Step 1:  
Write the Basic Equation:From the picture, we can see there is a triangle involving both the bug and the point (3,4). From this, we can see that
Retrieved from "https://wiki.math.ucr.edu/index.php?title=009A_Sample_Final_A,_Problem_9&oldid=130"