Difference between revisions of "009B Sample Final 1, Problem 5"
Jump to navigation
Jump to search
| Line 35: | Line 35: | ||
|- | |- | ||
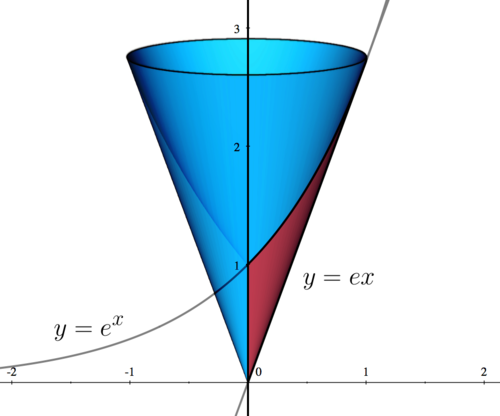
|First, we sketch the region bounded by the three functions. The region is shown in red, while the revolved solid is shown in blue. | |First, we sketch the region bounded by the three functions. The region is shown in red, while the revolved solid is shown in blue. | ||
| + | |- | ||
| + | | | ||
|- | |- | ||
|[[File:9BF1 5 GP.png|center|500px]] | |[[File:9BF1 5 GP.png|center|500px]] | ||
Revision as of 22:25, 26 February 2016
Consider the solid obtained by rotating the area bounded by the following three functions about the -axis:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=e^x} , and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=ex} .
a) Sketch the region bounded by the given three functions. Find the intersection point of the two functions:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=e^x} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=ex} . (There is only one.)
b) Set up the integral for the volume of the solid.
c) Find the volume of the solid by computing the integral.
| Foundations: |
|---|
| Recall: |
| 1. You can find the intersection points of two functions, say Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x),g(x),} |
|
| 2. The volume of a solid obtained by rotating an area around the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} -axis using cylindrical shells is given by |
|
Solution:
(a)
| Step 1: |
|---|
| First, we sketch the region bounded by the three functions. The region is shown in red, while the revolved solid is shown in blue. |
| Step 2: |
|---|
| Setting the equations equal, we have Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^x=ex} . |
| We get one intersection point, which is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1,e)} . |
| This intersection point can be seen in the graph shown in Step 1. |
(b)
| Step 1: |
|---|
| We proceed using cylindrical shells. The radius of the shells is given by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=x} . |
| The height of the shells is given by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h=e^x-ex} . |
| Step 2: |
|---|
| So, the volume of the solid is |
|
(c)
| Step 1: |
|---|
| We need to integrate |
|
| Step 2: |
|---|
| For the first integral, we need to use integration by parts. |
| Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u=x} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dv=e^xdx} . Then, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle du=dx} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v=e^x} . |
| So, the integral becomes |
|
| Final Answer: |
|---|
| (a) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1,e)} (See Step 1 for the graph) |
| (b) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_0^1 2\pi x(e^x-ex)~dx} |
| (c) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\pi-\frac{2\pi e}{3}} |