Difference between revisions of "009B Sample Final 1, Problem 5"
Jump to navigation
Jump to search
(Created page with "<span class="exam"> Consider the solid obtained by rotating the area bounded by the following three functions about the <math style="vertical-align: -3px">y</math>-axis: ::::...") |
|||
| Line 34: | Line 34: | ||
!Step 1: | !Step 1: | ||
|- | |- | ||
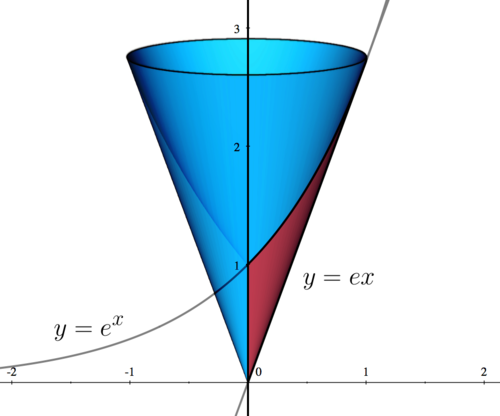
| − | |First, we sketch the region bounded by the three functions. | + | |First, we sketch the region bounded by the three functions. The region is shown in red, while the revolved solid is shown in blue. |
|- | |- | ||
| − | | | + | |[[File:9BF1 5 GP.png|center|500px]] |
|} | |} | ||
Revision as of 21:56, 26 February 2016
Consider the solid obtained by rotating the area bounded by the following three functions about the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} -axis:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=0} , Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=e^x} , and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=ex} .
a) Sketch the region bounded by the given three functions. Find the intersection point of the two functions:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=e^x} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=ex} . (There is only one.)
b) Set up the integral for the volume of the solid.
c) Find the volume of the solid by computing the integral.
| Foundations: |
|---|
| Recall: |
| 1. You can find the intersection points of two functions, say Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x),g(x),} |
|
| 2. The volume of a solid obtained by rotating an area around the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} -axis using cylindrical shells is given by |
|
Solution:
(a)
| Step 1: |
|---|
| First, we sketch the region bounded by the three functions. The region is shown in red, while the revolved solid is shown in blue. |
| Step 2: |
|---|
| Setting the equations equal, we have Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^x=ex} . |
| We get one intersection point, which is Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1,e)} . |
| This intersection point can be seen in the graph shown in Step 1. |
(b)
| Step 1: |
|---|
| We proceed using cylindrical shells. The radius of the shells is given by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle r=x} . |
| The height of the shells is given by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle h=e^x-ex} . |
| Step 2: |
|---|
| So, the volume of the solid is |
|
(c)
| Step 1: |
|---|
| We need to integrate |
|
| Step 2: |
|---|
| For the first integral, we need to use integration by parts. |
| Let Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u=x} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dv=e^xdx} . Then, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle du=dx} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle v=e^x} . |
| So, the integral becomes |
|
| Final Answer: |
|---|
| (a) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (1,e)} (See Step 1 for the graph) |
| (b) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_0^1 2\pi x(e^x-ex)~dx} |
| (c) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2\pi-\frac{2\pi e}{3}} |