Difference between revisions of "022 Sample Final A, Problem 13"
Jump to navigation
Jump to search
(Created page with "<span class="exam">Use differentials to find <math style="vertical-align: -4px">dy</math> given <math style="vertical-align: -4px">y = x^2 - 6x, ~ x = 4, ~dx = -0.5.</math> {...") |
|||
| Line 1: | Line 1: | ||
| + | [[File:Differential.png|right|400px]] | ||
| + | |||
<span class="exam">Use differentials to find <math style="vertical-align: -4px">dy</math> given <math style="vertical-align: -4px">y = x^2 - 6x, ~ x = 4, ~dx = -0.5.</math> | <span class="exam">Use differentials to find <math style="vertical-align: -4px">dy</math> given <math style="vertical-align: -4px">y = x^2 - 6x, ~ x = 4, ~dx = -0.5.</math> | ||
| Line 14: | Line 16: | ||
::<math>dy\,=\,f'(x)\cdot dx,</math> | ::<math>dy\,=\,f'(x)\cdot dx,</math> | ||
|- | |- | ||
| − | |where we use | + | |where we use the given specific <math style="vertical-align: 0px">x</math>-value to evaluate <math style="vertical-align: -5px">f'(x)</math>. |
Revision as of 20:41, 4 June 2015
Use differentials to find given Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y = x^2 - 6x, ~ x = 4, ~dx = -0.5.}
| Foundations: |
|---|
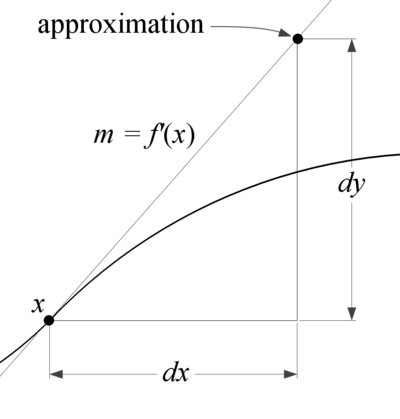
| When we use differentials, we are approximating a value for a function by using the slope of the derivative. The idea is that given a distance Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dx} from a point Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} , we can use Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'(x)} , the slope of the tangent line, to find the rise, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle dy} . Recalling that we can write |
|
| the relation is |
|
| where we use the given specific Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x}
-value to evaluate Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'(x)}
.
|
Solution:
| Step 1: |
|---|
| By the power rule, we have |
|
| We need to evaluate this at the given value Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=4} , so |
|
| Step 2: |
|---|
| We use the values given and the result from step 1 to find |
|
| Final Answer: |
|---|
|