Difference between revisions of "009B Sample Final 1, Problem 3"
Jump to navigation
Jump to search
| Line 82: | Line 82: | ||
!Final Answer: | !Final Answer: | ||
|- | |- | ||
| − | |'''(a)''' <math>(0,0),\bigg(\frac{\pi}{2},1\bigg),\bigg(\frac{-\pi}{2},-1\bigg)</math> | + | | '''(a)''' <math>(0,0),\bigg(\frac{\pi}{2},1\bigg),\bigg(\frac{-\pi}{2},-1\bigg)</math> |
|- | |- | ||
| − | |'''(b)''' <math>-\frac{\pi}{2}+2</math> | + | | '''(b)''' <math>-\frac{\pi}{2}+2</math> |
|} | |} | ||
[[009B_Sample_Final_1|'''<u>Return to Sample Exam</u>''']] | [[009B_Sample_Final_1|'''<u>Return to Sample Exam</u>''']] | ||
Revision as of 14:10, 18 April 2016
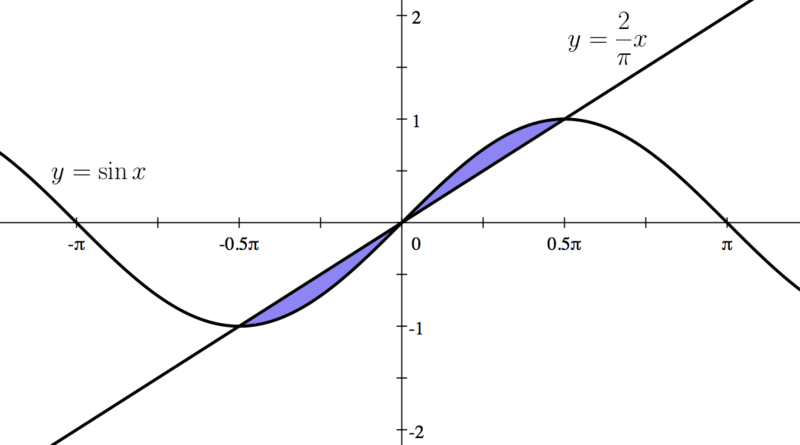
Consider the area bounded by the following two functions:
- and
- a) Find the three intersection points of the two given functions. (Drawing may be helpful.)
- b) Find the area bounded by the two functions.
| Foundations: |
|---|
| Recall: |
|
|
|
|
Solution:
(a)
| Step 1: |
|---|
| First, we graph these two functions. |
| Step 2: |
|---|
| Setting we get three solutions: |
|
|
| So, the three intersection points are |
| You can see these intersection points on the graph shown in Step 1. |
(b)
| Step 1: |
|---|
| Using symmetry of the graph, the area bounded by the two functions is given by |
|
|
| Step 2: |
|---|
| Lastly, we integrate to get |
|
|
| Final Answer: |
|---|
| (a) |
| (b) |