Difference between revisions of "009A Sample Final 1, Problem 7"
Jump to navigation
Jump to search
| Line 88: | Line 88: | ||
!Final Answer: | !Final Answer: | ||
|- | |- | ||
| − | |'''(a)'''  <math>\frac{dy}{dx}=\frac{3x^2-6y}{6x-3y^2}</math> | + | | '''(a)'''  <math>\frac{dy}{dx}=\frac{3x^2-6y}{6x-3y^2}</math> |
|- | |- | ||
| − | |'''(b)'''  <math>y=-1(x-3)+3</math> | + | | '''(b)'''  <math>y=-1(x-3)+3</math> |
|} | |} | ||
[[009A_Sample_Final_1|'''<u>Return to Sample Exam</u>''']] | [[009A_Sample_Final_1|'''<u>Return to Sample Exam</u>''']] | ||
Revision as of 14:15, 18 April 2016
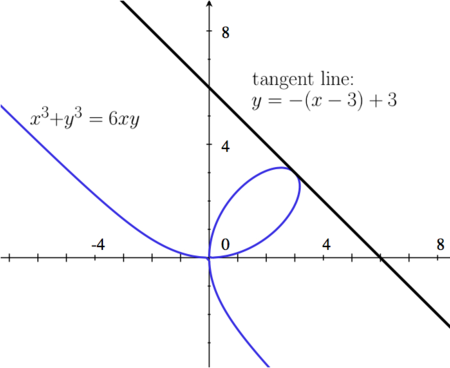
A curve is defined implicitly by the equation
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^3+y^3=6xy.}
- a) Using implicit differentiation, compute .
- b) Find an equation of the tangent line to the curve Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^3+y^3=6xy} at the point Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (3,3)} .
| Foundations: |
|---|
| 1. What is the result of implicit differentiation of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle xy?} |
|
| 2. What two pieces of information do you need to write the equation of a line? |
|
| 3. What is the slope of the tangent line of a curve? |
|
Solution:
(a)
| Step 1: |
|---|
| Using implicit differentiation on the equation Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x^3+y^3=6xy,} we get |
|
| Step 2: |
|---|
| Now, we move all the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dy}{dx}} terms to one side of the equation. |
| So, we have |
|
| We solve to get |
|
(b)
| Step 1: |
|---|
| First, we find the slope of the tangent line at the point Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (3,3).} |
| We plug Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (3,3)} into the formula for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dy}{dx}} we found in part (a). |
| So, we get |
|
| Step 2: |
|---|
| Now, we have the slope of the tangent line at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (3,3)} and a point. |
| Thus, we can write the equation of the line. |
| So, the equation of the tangent line at Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (3,3)} is |
|
| Final Answer: |
|---|
| (a) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dy}{dx}=\frac{3x^2-6y}{6x-3y^2}} |
| (b) Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=-1(x-3)+3} |