Difference between revisions of "009A Sample Final A, Problem 9"
(Created page with "<span style="font-size:135%"> <font face=Times Roman> 9. A bug is crawling along the <math style="vertical-align: 0%;">x</math>-axis at a constant speed of <math style...") |
|||
| Line 1: | Line 1: | ||
| + | [[File:BugGP.png|right|300px]] | ||
| + | |||
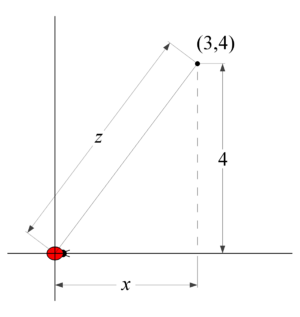
<span style="font-size:135%"> <font face=Times Roman> 9. A bug is crawling along the <math style="vertical-align: 0%;">x</math>-axis at a constant speed of <math style="vertical-align: -42%;">\frac{dx}{dt}=30</math>. | <span style="font-size:135%"> <font face=Times Roman> 9. A bug is crawling along the <math style="vertical-align: 0%;">x</math>-axis at a constant speed of <math style="vertical-align: -42%;">\frac{dx}{dt}=30</math>. | ||
How fast is the distance between the bug and the point <math style="vertical-align: -14%;">(3,4)</math> changing | How fast is the distance between the bug and the point <math style="vertical-align: -14%;">(3,4)</math> changing | ||
Revision as of 21:36, 23 March 2015
9. A bug is crawling along the Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x}
-axis at a constant speed of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{dx}{dt}=30}
.
How fast is the distance between the bug and the point Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (3,4)}
changing
when the bug is at the origin? (Note that if the distance is decreasing, then you should have a negative answer).
| Foundations: |
|---|
| Like most geometric word problems, you should start with a picture. This will help you declare variables and write meaningful equation(s). In this case, we will have to use implicit differentiation to arrive at our related rate. |
Solution:
| Part (a): |
|---|
| We need to find two values a and b such that one is positive, and one is negative. Notice that f(0) = √2, which is greater than zero. We can choose x = -1, to find f(-1) = -2 - 4 + √2, which is less than zero. Since f is clearly continuous, the IVT tells us there exists a c between -1 and 0 such that f(c) = 0. |