009A Sample Final 1, Problem 7

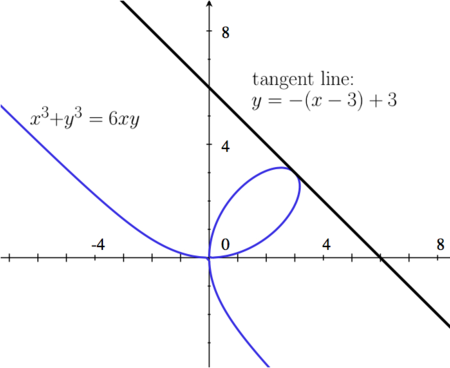
A curve is defined implicitly by the equation

$x^{3}+y^{3}=6xy.$

a) Using implicit differentiation, compute  ${\frac {dy}{dx}}$.

b) Find an equation of the tangent line to the curve $x^{3}+y^{3}=6xy$ at the point $(3,3)$.

Foundations:
1. What is the result of implicit differentiation of $xy?$
It would be  $y+x{\frac {dy}{dx}}$  by the Product Rule.
2. What two pieces of information do you need to write the equation of a line?
You need the slope of the line and a point on the line.
3. What is the slope of the tangent line of a curve?
The slope is  $m={\frac {dy}{dx}}.$

Solution:

(a)

Step 1:
Using implicit differentiation on the equation  $x^{3}+y^{3}=6xy,$ we get
$3x^{2}+3y^{2}{\frac {dy}{dx}}=6y+6x{\frac {dy}{dx}}.$

Step 2:
Now, we move all the  ${\frac {dy}{dx}}$  terms to one side of the equation.
So, we have
$3x^{2}-6y={\frac {dy}{dx}}(6x-3y^{2}).$
We solve to get
${\frac {dy}{dx}}={\frac {3x^{2}-6y}{6x-3y^{2}}}.$

(b)

Step 1:
First, we find the slope of the tangent line at the point  $(3,3).$
We plug $(3,3)$  into the formula for  ${\frac {dy}{dx}}$  we found in part (a).
So, we get
$m\,=\,{\frac {3(3)^{2}-6(3)}{6(3)-3(3)^{2}}}\,=\,{\frac {9}{-9}}\,=\,-1.$

Step 2:
Now, we have the slope of the tangent line at $(3,3)$  and a point.
Thus, we can write the equation of the line.
So, the equation of the tangent line at $(3,3)$  is
$y\,=\,-1(x-3)+3.$

Final Answer:
(a)  ${\frac {dy}{dx}}={\frac {3x^{2}-6y}{6x-3y^{2}}}$
(b)  $y=-1(x-3)+3$

Return to Sample Exam