009B Sample Final 1, Problem 5

Consider the solid obtained by rotating the area bounded by the following three functions about the $y$-axis:

$x=0$, $y=e^{x}$, and $y=ex$.

a) Sketch the region bounded by the given three functions. Find the intersection point of the two functions:

$y=e^{x}$ and $y=ex$. (There is only one.)

b) Set up the integral for the volume of the solid.

c) Find the volume of the solid by computing the integral.

Foundations:
Recall:
1. You can find the intersection points of two functions, say $f(x),g(x),$
by setting $f(x)=g(x)$ and solving for $x.$
2. The volume of a solid obtained by rotating an area around the $y$-axis using cylindrical shells is given by
$\int 2\pi rh~dx,$ where $r$ is the radius of the shells and $h$ is the height of the shells.

Solution:

(a)

Step 1:
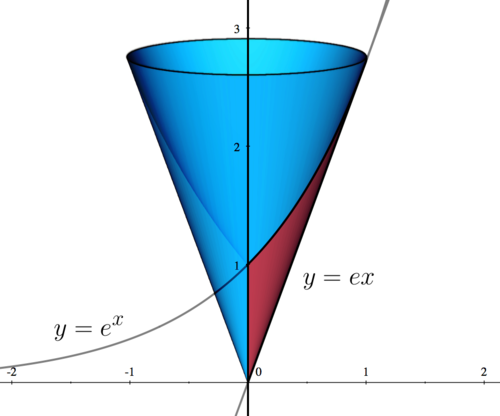
First, we sketch the region bounded by the three functions. The region is shown in red, while the revolved solid is shown in blue.

Step 2:
Setting the equations equal, we have $e^{x}=ex.$
We get one intersection point, which is $(1,e).$
This intersection point can be seen in the graph shown in Step 1.

(b)

Step 1:
We proceed using cylindrical shells. The radius of the shells is given by $r=x.$
The height of the shells is given by
$h=e^{x}-ex.$

Step 2:
So, the volume of the solid is
$\int 2\pi rh\,dx\,=\,\int _{0}^{1}2\pi x(e^{x}-ex)\,dx.$

(c)

Step 1:
We need to integrate
$\int _{0}^{1}2\pi x(e^{x}-ex)\,dx\,=\,2\pi \int _{0}^{1}xe^{x}\,dx-2\pi \int _{0}^{1}ex^{2}\,dx.$

Step 2:
For the first integral, we need to use integration by parts.
Let $u=x$ and $dv=e^{x}dx.$ Then, $du=dx$ and $v=e^{x}.$
So, the integral becomes
${\begin{array}{rcl}\displaystyle {\int _{0}^{1}2\pi x(e^{x}-ex)~dx}&=&\displaystyle {2\pi {\bigg (}xe^{x}{\bigg |}_{0}^{1}-\int _{0}^{1}e^{x}dx{\bigg )}-{\frac {2\pi ex^{3}}{3}}{\bigg |}_{0}^{1}}\\&&\\&=&\displaystyle {2\pi {\bigg (}xe^{x}-e^{x}{\bigg )}{\bigg |}_{0}^{1}-{\frac {2\pi e}{3}}}\\&&\\&=&\displaystyle {2\pi (e-e-(-1))-{\frac {2\pi e}{3}}}\\&&\\&=&\displaystyle {2\pi -{\frac {2\pi e}{3}}}.\\\end{array}}$

Final Answer:
(a)  $(1,e)$ (See Step 1 for the graph)
(b)  $\int _{0}^{1}2\pi x(e^{x}-ex)~dx$
(c)  $2\pi -{\frac {2\pi e}{3}}$

Return to Sample Exam