|
|
| Line 1: |
Line 1: |
| | <span class="exam">Consider the region bounded by the following two functions: | | <span class="exam">Consider the region bounded by the following two functions: |
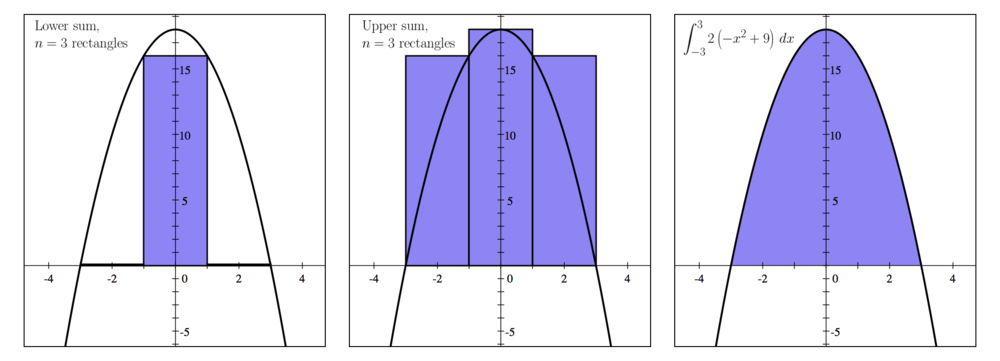
| − | ::::::::<span class="exam"> <math style="vertical-align: -5px">y=2(-x^2+9)</math> and <math style="vertical-align: -4px">y=0</math>.
| + | ::::::<span class="exam"> <math style="vertical-align: -5px">y=2(-x^2+9)</math> and <math style="vertical-align: -4px">y=0.</math> |
| | | | |
| − | <span class="exam">a) Using the lower sum with three rectangles having equal width, approximate the area. | + | ::<span class="exam">a) Using the lower sum with three rectangles having equal width, approximate the area. |
| | | | |
| − | <span class="exam">b) Using the upper sum with three rectangles having equal width, approximate the area. | + | ::<span class="exam">b) Using the upper sum with three rectangles having equal width, approximate the area. |
| | | | |
| − | <span class="exam">c) Find the actual area of the region. | + | ::<span class="exam">c) Find the actual area of the region. |
| | | | |
| | {| class="mw-collapsible mw-collapsed" style = "text-align:left;" | | {| class="mw-collapsible mw-collapsed" style = "text-align:left;" |
Revision as of 11:36, 18 April 2016
Consider the region bounded by the following two functions:
-
 and
and 
- a) Using the lower sum with three rectangles having equal width, approximate the area.
- b) Using the upper sum with three rectangles having equal width, approximate the area.
- c) Find the actual area of the region.
| Foundations:
|
| Recall:
|
1. The height of each rectangle in the lower Riemann sum is given by choosing the minimum  value of the left and right endpoints of the rectangle. value of the left and right endpoints of the rectangle.
|
2. The height of each rectangle in the upper Riemann sum is given by choosing the maximum  value of the left and right endpoints of the rectangle. value of the left and right endpoints of the rectangle.
|
3. The area of the region is given by  for appropriate values for appropriate values  . .
|
Solution:
(a)
| Step 1:
|
| We need to set these two equations equal in order to find the intersection points of these functions.
|
So, we let  . Solving for . Solving for  , we get , we get  . .
|
This means that we need to calculate the Riemann sums over the interval ![{\displaystyle [-3,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a869f6f7ff84a95f888c6b8705e2465ba21960e) . .
|
|
|
| Step 2:
|
Since the length of our interval is  and we are using and we are using  rectangles, rectangles,
|
each rectangle will have width  . .
|
| Thus, the lower Riemann sum is
|

|
(b)
| Step 1:
|
As in Part (a), the length of our inteval is  and and
|
each rectangle will have width  . (See Step 1 and 2 for (a)) . (See Step 1 and 2 for (a))
|
| Step 2:
|
| Thus, the upper Riemann sum is
|

|
(c)
| Step 1:
|
| To find the actual area of the region, we need to calculate
|

|
| Step 2:
|
| We integrate to get
|

|
| Final Answer:
|
(a) 
|
(b) 
|
(c) 
|
Return to Sample Exam








![{\displaystyle [-3,3]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a869f6f7ff84a95f888c6b8705e2465ba21960e)