Difference between revisions of "009B Sample Final 1, Problem 3"
Jump to navigation
Jump to search
(Created page with "<span class="exam">Consider the area bounded by the following two functions: ::::::<math>y=\sin x</math> and <math style="vertical-align: -13px">y=\frac{2}{\pi}x.</math> <sp...") |
|||
| Line 31: | Line 31: | ||
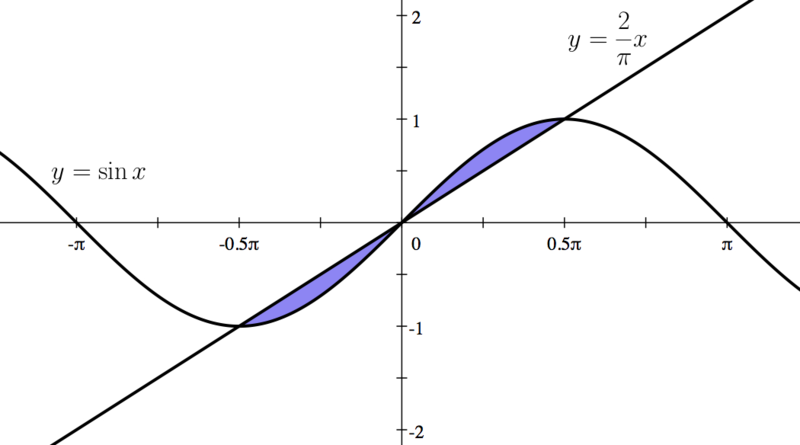
|First, we graph these two functions. | |First, we graph these two functions. | ||
|- | |- | ||
| − | | | + | |[[File:9BF1 3 GP.png|center|800px]]|} |
| − | |} | ||
{| class="mw-collapsible mw-collapsed" style = "text-align:left;" | {| class="mw-collapsible mw-collapsed" style = "text-align:left;" | ||
Revision as of 21:50, 26 February 2016
Consider the area bounded by the following two functions:
- Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=\sin x} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=\frac{2}{\pi}x.}
a) Find the three intersection points of the two given functions. (Drawing may be helpful.)
b) Find the area bounded by the two functions.
| Foundations: |
|---|
| Recall: |
| 1. You can find the intersection points of two functions, say Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x),g(x),} |
|
| 2. The area between two functions, Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(x)} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(x)} , is given by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \int_a^b f(x)-g(x)~dx} |
|
Solution:
(a)
| Step 1: | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| First, we graph these two functions. | ||||||||||||||
|}
(b)
|