008A Sample Final A, Question 6

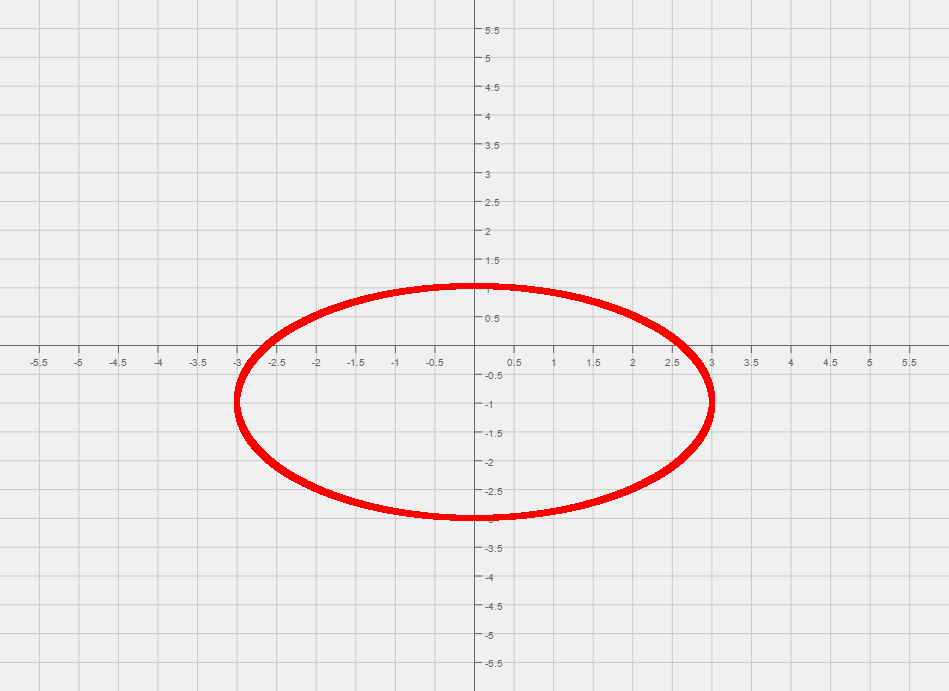
Question: Sketch $4x^{2}+9(y+1)^{2}=36$. Give coordinates of each of the 4 vertices of the graph.

Foundations:
1) What type of function is this?
2) What can you say about the orientation of the graph?
Answer:
1) Since both x and y are squared it must be a hyperbola or an ellipse. We can conclude that the graph is an ellipse since both $x^{2}$   and   $y^{2}$ have the same sign, positive.
2) Since the coefficient of the $x^{2}$ term is smaller, when we divide both sides by 36 the X-axis will be the major axis.

Solution:

Step 1:
We start by dividing both sides by 36. This yields ${\frac {4x^{2}}{36}}+{\frac {9(y+1)^{2}}{36}}={\frac {x^{2}}{9}}+{\frac {(y+1)^{2}}{4}}=1$.

Step 2:
Now that we have the equation that looks like an ellipse, we can read off the center of the ellipse, (0, -1).
From the center mark the two points that are 3 units left, and three units right of the center.
Then mark the two points that are 2 units up, and two units down from the center.

Final Answer:
The four vertices are: $(-3,-1),(3,-1),(0,1){\text{ and }}(0,-3)$

Return to Sample Exam