Difference between revisions of "022 Exam 2 Sample A, Problem 10"
Jump to navigation
Jump to search
| Line 7: | Line 7: | ||
!Foundations: | !Foundations: | ||
|- | |- | ||
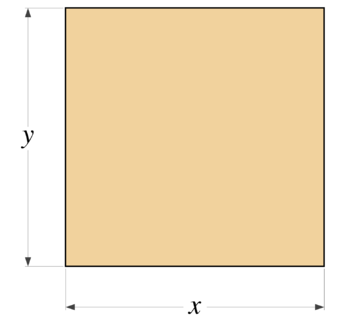
| − | |As with all word problems, start with a picture. Using the variables <math style="vertical-align: 0%">x</math> and <math style="vertical-align: -20%">y</math> as shown in the image, we need to remember the equations of a rectangle for perimeter: | + | |As with all geometric word problems, it helps to start with a picture. Using the variables <math style="vertical-align: 0%">x</math> and <math style="vertical-align: -20%">y</math> as shown in the image, we need to remember the equations of a rectangle for perimeter: |
|- | |- | ||
| | | | ||
Latest revision as of 09:46, 16 May 2015
Use calculus to set up and solve the word problem: Find the length and width of a rectangle that has a perimeter of 48 meters and maximum area.
| Foundations: |
|---|
| As with all geometric word problems, it helps to start with a picture. Using the variables and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} as shown in the image, we need to remember the equations of a rectangle for perimeter: |
|
| and for area: |
|
| Since we want to maximize area, we will have to rewrite it as a function of a single variable, and then find when the first derivative is zero. From this, we will find the dimensions which provide the maximum area. |
Solution:
| Step 1: |
|---|
| Express one variable in terms of the other: Since we know that the perimeter is to be 48 meters and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle P\,=\,2x+2y} , we can solve for Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} in terms of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} . Since |
|
| we find that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=24-x.} |
| Step 2: |
|---|
| Find an expression for area in terms of one variable: Now, we can use the substitution from part 1 to find |
|
| Step 3: |
|---|
| Find the derivative and its roots: Since Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle A(x)=24x-x^2} , we have |
|
| This derivative is zero precisely when Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=y=12} , and these are the values that will maximize area. Also, don't forget the units - meters! |
| Final Answer: |
|---|
| The area is maximized when both the length and width are 12 meters. |