Difference between revisions of "022 Exam 2 Sample A, Problem 8"
Jump to navigation
Jump to search
(Created page with "Use differentials to approximate the change in profit given <math style="vertical-align: -5%">x = 10</math> units and <math style="vertical-align: 0%">dx = 0.2</math>&...") |
|||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | Use differentials to approximate the change in profit given <math style="vertical-align: -5%">x = 10</math>  units and <math style="vertical-align: 0%">dx = 0.2</math>  units, where profit is given by <math style="vertical-align: -23%">P(x) = -4x^2 + 90x - 128</math>. | + | [[File:022_2_A_8.png|right|400px]] |
| + | <span class="exam">Use differentials to approximate the change in profit given <math style="vertical-align: -5%">x = 10</math>  units and <math style="vertical-align: 0%">dx = 0.2</math>  units, where profit is given by <math style="vertical-align: -23%">P(x) = -4x^2 + 90x - 128</math>. | ||
{| class="mw-collapsible mw-collapsed" style = "text-align:left;" | {| class="mw-collapsible mw-collapsed" style = "text-align:left;" | ||
!Foundations: | !Foundations: | ||
|- | |- | ||
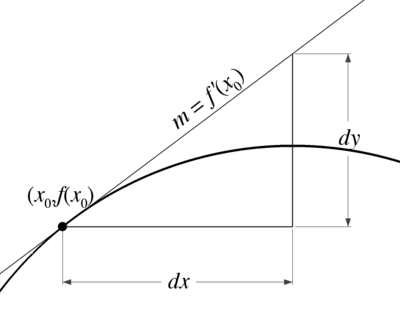
| − | |A differential is a method of approximating a | + | |A differential is a method of linearly approximating the change of a function. We use the derivative of the function at an initial point <math style="vertical-align: 0%">x_0</math> as the slope of a line, and use the standard relation |
|- | |- | ||
| | | | ||
| − | ::<math>\ | + | ::<math>m\,=\,\frac{\Delta y}{\Delta x},</math> |
|- | |- | ||
| − | | | + | |where <math style="vertical-align: -20%">\Delta y</math> represents the change in <math style="vertical-align: -20%">y</math> values, and <math style="vertical-align: 0%">\Delta x</math> represents the change in <math style="vertical-align: 0%">x</math> values. Due to the use of the derivative <math style="vertical-align: -22%">f'\left(x_0\right)</math> as the slope, we usually rewrite this using <math>dy</math> and <math style="vertical-align: 0%">dx</math> to indicate the relative changes. Thus, |
| + | |- | ||
| + | | | ||
| + | ::<math>f'(x_0)\,=\,m\,=\,\frac{dy}{dx}.</math> | ||
| + | |- | ||
| + | |We can then rearrange this to find <math>dy=f'(x_0)\cdot dx.</math> | ||
| + | |- | ||
| + | |||
|} | |} | ||
| Line 17: | Line 25: | ||
!Step 1: | !Step 1: | ||
|- | |- | ||
| − | | | + | |First, we must find the derivative. We have <math style="vertical-align: -23%">P'(x) = -8x + 90</math>. |
|} | |} | ||
{| class="mw-collapsible mw-collapsed" style = "text-align:left;" | {| class="mw-collapsible mw-collapsed" style = "text-align:left;" | ||
!Step 2: | !Step 2: | ||
| + | |- | ||
| + | |We need the derivative at our initial point, or <math style="vertical-align: -15%">x_0 = 10</math>. This is | ||
| + | |- | ||
| + | | | ||
| + | ::<math>P'(x_0)\,=\,P'(10) \,=\, -8(10) + 90\,=\,10.</math> | ||
| + | |} | ||
| + | {| class="mw-collapsible mw-collapsed" style = "text-align:left;" | ||
| + | !Step 3: | ||
| + | |- | ||
| + | |Finally, we plug in the values to find | ||
|- | |- | ||
| | | | ||
| + | ::<math>dy\,=\,P'(x_0)\cdot dx\,=\,10\cdot 0.2\,=\,2.</math> | ||
| + | |- | ||
| + | |Note that if a teacher gives you units (thousands of dollars, dollars, cubits...), you should include them in your answer. | ||
| + | |} | ||
| + | {| class="mw-collapsible mw-collapsed" style = "text-align:left;" | ||
| + | !Final Answer: | ||
| + | |- | ||
| + | | | ||
| + | ::<math>dy\,=\,2.</math> | ||
|} | |} | ||
| − | |||
[[022_Exam_2_Sample_A|'''<u>Return to Sample Exam</u>''']] | [[022_Exam_2_Sample_A|'''<u>Return to Sample Exam</u>''']] | ||
Latest revision as of 20:13, 15 May 2015
Use differentials to approximate the change in profit given units and units, where profit is given by .
| Foundations: |
|---|
| A differential is a method of linearly approximating the change of a function. We use the derivative of the function at an initial point as the slope of a line, and use the standard relation |
|
|
| where represents the change in values, and represents the change in values. Due to the use of the derivative as the slope, we usually rewrite this using and to indicate the relative changes. Thus, |
|
|
| We can then rearrange this to find |
Solution:
| Step 1: |
|---|
| First, we must find the derivative. We have . |
| Step 2: |
|---|
| We need the derivative at our initial point, or . This is |
|
|
| Step 3: |
|---|
| Finally, we plug in the values to find |
|
|
| Note that if a teacher gives you units (thousands of dollars, dollars, cubits...), you should include them in your answer. |
| Final Answer: |
|---|
|
|