Difference between revisions of "009A Sample Final A, Problem 7"

Latest revision as of 08:53, 2 April 2015

7. A farmer wishes to make 4 identical rectangular pens, each with 500 sq. ft. of area. What dimensions for each pen will use the least amount of total fencing?

Foundations:
As a word problem, we must begin by assigning variables in order to construct useful equation(s). As an optimization problem, we will be taking a derivative of one of our equations in order to find an extreme point.

Solution:

Step 1:

Declare Variables: We are attempting to find the dimensions of a single pen, such that we use as little fencing as possible for all four pens. Let's use Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} and Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} as indicated in the image, and simply call the length of fencing required Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L} .

Step 2:

Form the Equations: Notice that we need fencing between each of the pens, so we require a total of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 5} pieces of length Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y} . We also need Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 2} pieces of length Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} for each pen, which means there are a total of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 4\cdot 2} pieces required of length Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x} . Together, we need a total length of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L=8x+5y} .

On the other hand, we know that each pen has a fixed area of Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 500} square feet. Thus, we also know that Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle xy=500} .

Step 3:
Optimize: Since Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle xy=500} , we also know Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y=500/x} . Plugging this into our equation for length, we have
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L(x) = 8x + 5\cdot \frac{500}{x} = 8x + \frac{2500}{x}.}
We now take the derivative to find
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle L'(x)=8-\frac{2500}{x^2}= \frac{8x^2-2500}{x^2}.}
The denominator can never be zero, and if we set the numerator to zero we find
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x=\pm\sqrt{\frac{2500}{8}} = \pm\frac{50}{2\sqrt{2}} =\pm\frac{\,\,25}{\sqrt{2}}.}
Of course, we can't have negative fencing lengths, so we can ignore the negative root. Finally, we use the area relation to find
Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle y =\frac{500}{25\sqrt{2}} = \frac{500\sqrt{2}}{25} = 20\sqrt{2}. }
Thus, the least amount of fencing is used when we size our Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 500} sq. ft. pens as Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 20\sqrt{2}} feet by Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle 25/\sqrt{2}} feet.

Return to Sample Exam

@@ Line 1: / Line 1: @@
+[[File:009A_SF_A_7_PensDim.png|right|200px]]
 <br>
 <span style="font-size:135%"><font face=Times Roman>  7. A farmer wishes to make 4 identical rectangular pens, each with
@@ Line 9: / Line 10: @@
 |As a word problem, we must begin by assigning variables in order to construct useful equation(s).  As an optimization problem, we will be taking a derivative of one of our equations in order to find an extreme point.
 |}
-'''Solution:'''
+&nbsp;'''Solution:'''
 {| class="mw-collapsible mw-collapsed" style = "text-align:left;"
-!Part (a): &nbsp;
+!Step 1: &nbsp;
+|-
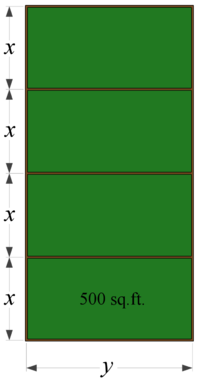
+|'''Declare Variables:''' &nbsp; We are attempting to find the dimensions of a single pen, such that we use as little fencing as possible for all four pens.  Let's use <math style="vertical-align: 0%;">x</math> and <math style="vertical-align: -18%;">y</math> as indicated in the image, and simply call the length of fencing required <math style="vertical-align: 1%;">L</math>.
+|}
+{| class="mw-collapsible mw-collapsed" style = "text-align:left;"
+!Step 2: &nbsp;
+|-
+|'''Form the Equations:''' &nbsp; Notice that we need fencing between each of the pens, so we require a total of <math style="vertical-align: 0%;">5</math> pieces of length <math style="vertical-align: -18%;">y</math>. We also need <math style="vertical-align: 0%;">2</math> pieces of length <math style="vertical-align: 0%;">x</math> for each pen, which means there are a total of <math style="vertical-align: -5%;">4\cdot 2</math> &thinsp; pieces required of length <math style="vertical-align: 0%;">x</math>. Together, we need a total length of <math style="vertical-align: -18%;">L=8x+5y</math>.
+|-
+|On the other hand, we know that each pen has a fixed area of <math style="vertical-align: 0%;">500</math> square feet.  Thus, we also know that <math style="vertical-align: -18%;">xy=500</math>.
+|}
+{| class="mw-collapsible mw-collapsed" style = "text-align:left;"
+!Step 3: &nbsp;
+|-
+|'''Optimize:''' &nbsp; Since <math style="vertical-align: -18%;">xy=500</math>, we also know <math style="vertical-align: -21%;">y=500/x</math>. Plugging this into our equation for length, we have
+|-
+|&nbsp;&nbsp;&nbsp;&nbsp; <math>L(x) = 8x + 5\cdot \frac{500}{x} = 8x + \frac{2500}{x}.</math>
+|-
+|We now take the derivative to find
+|-
+|&nbsp;&nbsp;&nbsp;&nbsp; <math>L'(x)=8-\frac{2500}{x^2}= \frac{8x^2-2500}{x^2}.</math>
+|-
+|The denominator can never be zero, and if we set the numerator to zero we find
+|-
+|&nbsp;&nbsp;&nbsp;&nbsp; <math>x=\pm\sqrt{\frac{2500}{8}} = \pm\frac{50}{2\sqrt{2}} =\pm\frac{\,\,25}{\sqrt{2}}.</math>
+|-
+|Of course, we can't have negative fencing lengths, so we can ignore the negative root.  Finally, we use the area relation to find
+|-
+|&nbsp;&nbsp;&nbsp;&nbsp; <math>y =\frac{500}{25\sqrt{2}} = \frac{500\sqrt{2}}{25} = 20\sqrt{2}. </math>
+|-
+|Thus, the least amount of fencing is used when we size our <math style="vertical-align: 0%;">500</math> sq. ft. pens as <math style="vertical-align: -8%;">20\sqrt{2}</math> feet by <math style="vertical-align: -22%;">25/\sqrt{2}</math> feet.
+|}
 [[009A_Sample_Final_A|'''<u>Return to Sample Exam</u>''']]

Difference between revisions of "009A Sample Final A, Problem 7"

Latest revision as of 08:53, 2 April 2015

Navigation menu

Search